Metodo a strati per principianti - Jasmine Lee



Questo è il bel metodo a strati per principianti proposto dalla cuber australiana Jasmine Lee.
È un classico metodo a strati che risolve il terzo strato in 4 passi usando 4 formule molto semplici e conosciute; fra i metodi per principianti è fra i più efficienti (formule brevi e facili) e a mio parere il più bello se pure lievissimamente più complicato di altri per via dei numerosi casi che si devono riconoscere nel passo 3 di orientamento degli angoli.


Il metodo originale viene descritto su questa pagina:
Jasmine Lee beginner solution for cube
di cui puoi anche leggere una traduzione in italiano


Rispetto al procedimento originale alcune formule sono traslate nella forma che io utilizzo normalmente.
Utilizzo anche un diverso approccio concettuale che mi pare più intuitivo nella risoluzione del passo della permutazione di tre angoli (passo 2), che quindi apparentemente sembra essere diverso da quanto proposto da Jasmine Lee ma in effetti la procedura rimane nella sostanza identica.

Nella risoluzione a strati la realizzazione dei primi due strati e totalmente separata dalla risoluzione del terzo strato; al solito separo in due pagine distinte la risoluzione dei primi due strati da quella dell'ultimo che di fatto caratterizza completamente ogni metodo a strati.

Il terzo strato si realizza in 4 passi:
• orientamento spigoli
• posizionamento angoli (Niklas)
• orientamento angoli (Sune)
• posizionamento spigoli (Allan)


Risoluzione del Terzo Strato

Nelle figure:
giallo: colore dell'ultima faccia
bianco: faccette ordinate di colore imprecisato
grigio chiaro: ancora da ordinare di colore imprecisato
grigio scuro: posizioni in fase di ordinamento (interessate dalla formula in esame) di colore imprecisato
il giallo è usato in luogo di uno degli altri tre colori quando sia possibile definirlo con certezza

Passo 1 - Forma la croce dell'ultimo strato (orienta gli spigoli)

Da ora in avanti la faccia che resta da risolvere sarà la nostra faccia U.

Consideriamo i soli spigoli; in questo passo si tratta di orientarli osservando solo il loro lato sulla faccia U prescindendo dal loro corretto posizionamento; cioè dobbiamo fare in modo di avere i colori degli spigoli sulla faccia Up tutti dello stesso colore della faccetta centrale Up senza occuparci del secondo colore di ogni spigolo.

Si possono avere le seguenti situazioni:
  • 1.1

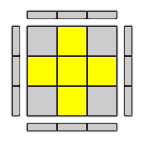
    I 4 spigoli sono orientati tutti correttamente.
    Il loro colore sulla faccia U corrisponde al colore della faccetta centrale su U: non fare nulla, la croce è già fatta;

    • vai al passo 2
  • 1.2

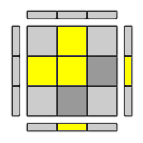
    2 spigoli adiacenti risultano ribaltati e gli altri 2 corretti:
    posiziona il cubo in modo che i 2 spigoli orientati correttamente siano in posizione UL e UB e i due spigoli ribaltati siano in posizione UF e UR e applica

    • F U R U' R' F'
      alternativa: x U R' U' Lw U R U' R'
    • vai al passo 2
  • 1.3

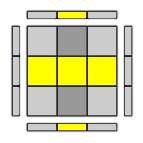
    2 soli spigoli in posizione opposta risultano ribaltati:
    posiziona il cubo in modo che i due spigoli orientati correttamente siano in posizione UL e UR e i 2 spigoli ribaltati in posizione UF e UB e applica

    • F R U R' U' F' (inversa della precedente)
      alternativa: R U R' U' R' F R F'
    • vai al passo 2
  • 1.4

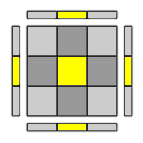
    I 4 spigoli risultano tutti ribaltati.
    mantenedo sempre la stessa faccia Up e con qualunque scelta per la faccia Front applica

    • F U R U' R' F' (o la sua inversa o una delle due alternative)
    • riapplica il Passo 1
    [Nota:
    La procedura del passo 1.4 si potrebbe esprimere semplicemente con
    - Applica F U R U' R' F' y' F R U R' U' F'
    - vai al passo 2]

Se il numero di spigoli ribaltati è dispari (1 o 3) smonta il cubo e rimontalo correttamente!

Passo 2 - Posiziona gli angoli dell'ultimo strato

Si tratta ora di posizionare i 4 angoli sulla faccia U; posizionarli significa metterli nella giusta posizione finale, senza però occuparsi del corretto orientamento; in conseguenza delle formule applicate gli spigoli si muoveranno dalle posizioni raggiunte nel passo precedente ma rimarranno comunque orientati correttamente.

Passo Preliminare:
Cerca un qualunque angolo orientato correttamente e mettilo nella sua giusta posizione ruotando la faccia Up; se nessun angolo è orientato correttamente scegline uno qualunque (non orientato) e, sempre ruotando opportunamente la faccia Up, mettilo nella sua giusta posizione.

A seconda della configurazione (stato) che trovi esegui uno dei seguenti passi:
  • 2.1

    I 4 angoli sono tutti nella posizione corretta; non occorre fare nulla;

    • vai al passo 3
  • 2.2

    • Un solo angolo è nella posizione corretta; occorre permutare gli altri tre angoli.
      Se devono permutare in senso antiorario posiziona l'angolo corretto in URF e applica la formula

      • (Niklas) (U) R U' L' U R' U' L
      • Vai al passo 3

    • se devono permutare in senso orario posiziona il cubo in modo che l'angolo corretto si trovi in ULF e usa la formula:

      • (Niklas simmetrica) (U') L' U R U' L U R'
      • Vai al passo 3
  • 2.3

    Due angoli adiacenti sono scambiati tra loro (e gli altri due sono in posizione corretta ma non necessariamente orientati)

    • Ruota la faccia Up di 90 gradi (esegui U o U') in modo da posizionare correttamente un solo angolo (gli altri tre angoli risulteranno quindi permutati tra loro)
    • applica il passo 2.2
    [ Brevemente il passo 2.3 si potrebbe esprimere con:
    - Esegui la formula:
    (Niklas) (U2) R U' L' U R' U' L
    - vai al passo 3     ]

  • 2.4

    Due angoli sulla diagonale sono scambiati tra loro (e gli altri due sono in posizione corretta ma non necessariamente orientati)

    • ruota la faccia Up di 90 gradi (esegui U oppure U'); questo porta i 4 angoli tutti fuori posto e si avranno due coppie di angoli adiacenti da scambiare
    • mantenendo sempre la stessa Up e con una qualunque scelta per la Front applica la formula per la permutazione di tre angoli:
      (U) R U' L' U R' U' L
      questo posizionerà correttamente un solo angolo, lasciando gli altri tre permutati
    • applica il passo 2.2
    [ brevemente il passo 2.4 con la scelta
    U' + (U) R U' L' U R' U' L diventa:
    - Esegui la formula:
    (Niklas) R U' L' U R' U' L
    - vai al passo 2.2     ]

Passo 3 - Orienta gli angoli dell'ultimo strato

Gli angoli nelle loro giuste posizioni devono ora essere orientati; esistono otto possibili configurazioni o stati; per orientare gli angoli si utilizza la Sune, una bella formula molto veloce da eseguire, la quale fa' permutare anche tre spigoli senza cambiarne l'orientamento, ma in questa fase la cosa non ci da' fastidio in quanto gli spigoli li posizioneremo solo nel passo successivo.
La U2 finale serve per chiudere la Sune in una formula completa e riposizionare gli angoli.
La Sune (con una sua inversa), orientando tre angoli, consente di risolvere in una sola "passata" solo due degli otto casi che si possono presentare; un altro caso è quello fortunato in cui gli angoli sono già tutti orientati; gli altri cinque casi dovranno essere risolti con una seconda "passata" (2-look).

  • 3.1

    i 4 angoli sono tutti orientati correttamente; non occorre fare nulla.

    • vai al Passo 4
  • 3.2
    un solo angolo è orientato correttamente; gli altri tre risulteranno ruotati tutti con spin +1/3 oppure tutti con spin -1/3.

    • Se i tre angoli hanno spin -1/3 posiziona il cubo mantenedo l'angolo orientato correttamente in ULF ed applica la formula:

      • (Sune) R U R' U R U2 R' (U2)
      • vai al passo 4

    • Se i tre angoli hanno spin +1/3 posiziona il cubo mantenedo l'angolo orientato correttamente in ULB ed applica la formula

      • (Sune simmetrica) R' U' R U' R' U2 R (U2)
      • vai al passo 4
  • 3.3
    due angoli risultano orientati scorrettamente (con spin opposti mentre gli altri due sono orientati correttamente); esistono tre sole possibili configurazioni a cui ricondursi

    posiziona il cubo come in una delle tre figure ed applica la formula:

    • R U R' U R U2 R' (U2)
      questo porterà ad uno stato con tre angoli ruotati su sé stessi con uguale spin
    • applica il passo 3.2
  • 3.4
    i 4 angoli sono tutti orientati male; due con spin +1/3 e due con spin -1/3 ; esistono due sole configurazioni possibili a cui ricondursi

    posiziona il cubo come in una delle due figure ed applica la formula:

    • R U R' U R U2 R' (U2)
      questo porterà ad uno stato con tre angoli ruotati su sé stessi con uguale spin
    • applica il passo 3.2
Se la somma degli spin degli angoli non da' 0 o un intero con segno smonta il cubo e rimontalo correttamente!

Passo 4 - Posiziona gli spigoli dell'ultimo strato

Si tratta ora di disporre gli spigoli messi a croce (già orientati) nella loro giusta posizione.
  • 4.1

    gli spigoli sono tutti corretti nelle loro posizioni

    • il cubo è finito.
  • 4.2
    Se un solo spigolo è in posizione corretta allora occorrerà far ruotare tra loro (permutare) gli altri tre spigoli:

    • posiziona il cubo in modo che lo spigolo corretto si trovi in UB se i rimanenti tre spigoli devono scambiarsi di posto (permutare) in senso orario e applica

      • (Allan) F2 U M' U2 M U F2
      • Finito!

    • posiziona il cubo in modo che lo spigolo corretto si trovi in UB se devono ruotare tra loro (permutare) in senso antiorario

      • (Allan simmetrica) F2 U' M' U2 M U' F2
      • Finito!
  • 4.3

    Se si presenta lo scambio di due coppie di spigoli opposti (in asse con la faccetta centrale) o adiacenti allora in entrambi i casi

    • Mantenendo l'ultima faccia su Up e con qualunque colore per la faccia Front
      Applica la permutazione di tre spigoli
      F2 U M' U2 M U F2
      o la sua simmetrica; questo metterà nella giusta posizione (mantenendo l'orientamento) un solo spigolo
    • Applica il passo 4.2
Se due soli spigoli sono nella posizione corretta e gli altri due sono scambiati di posto smonta il cubo e rimontalo correttamente!


Evoluzioni del metodo

Come già descritto nell'articolo originale vi sono diverse notevoli evoluzioni di questo metodo:
- imparare una tecnica F2L per risolvere in 4 passate i 4 slots angolo primo livello - corrispondente spigolo secondo livello
- imparare l'OLL Corners (Orient Last Layer Corners) (7 formule) utilizzando le formule derivate dal metodo di Lars Petrus (Vedi OLL angoli Fridrich semplificato - intermediate) per risolvere in una sola passata il passo 3 (orientamento angoli)
- imparare il set di formule per il PLL Edges (Permute Last Layer Edges) del Fridrich semplificato (Vedi PLL spigoli Fridrich semplificato - intermediate) per risolvere in una sola passata il passo 4 (posizionamento spigoli) imparando le formula per lo scambio di due coppie di spigoli adiacenti (senza cambiare l'orientamento) e quella per lo scambio di due coppie di spigoli opposti (senza cambiare l'orientamento)
- imparare la formula per lo scambio di due angoli adiacenti per risolvere in una sola passata il passo 2 di posizionamento degli angoli
- imparare la formula del passo 1.4 o una sua equivalente per risolvere in una sola passata il passo 1

Con queste ulteriori formule si ottiene un discreto metodo abbastanza veloce, paragonabile ad un Fridrich semplificato intermediate con cui si possono ottenere tempi di risoluzione tra 30 e 60 secondi.