Notazione
Definizione dei pezziSistema di riferimento
I colori
Notazioni utilizzate
Mosse della faccia (R, R', R2, ...)
Mosse del doppio strato esterno (Rw, Rw', Rw2, ...)
Mosse del solo strato interno (r, r', r2, ...)
Mosse dello strato intermedio (M, M', M2, E, S, ...)
Altre Notazioni (Rs, Ra, ...)
Orientamento dell'intero cubo (x, x', y, y', z, z')
Uso delle parentesi nelle formule
Individuare la posizione di un pezzo
Spostamento di un pezzo
Orientamento del pezzo
Posizionamento del pezzo
Disposizione del pezzo
Definizione dei Pezzi
Nel cubo ci sono 3 tipi di pezzi:6 faccette centrali con un solo lato o faccetta; tali faccette corrispondono alle 6 facce del cubo, nel senso che su ogni faccia del cubo è visibile una ed una sola faccetta centrale; tali faccette centrali determinano il colore dell'intera faccia.
12 spigoli (edges) ognuno dotato di due facce o faccette colorate.
8 angoli (corners) ognuno con tre facce o faccette colorate.
Utilizzo la dizione pezzo probabilmente da derivazione scacchistica; si potrebbero usare altri nomi come cubetto, elemento, blocchetto od altro, ma io preferisco il termine pezzo, in quanto trovo ci siano delle analogie con i pezzi della scacchiera; a volte comunque lo indicherò con cubetto (cubie).
Potrò anche riferirmi ad una faccetta (facelet) di un pezzo per riferirmi ad una delle facce "visibili" costituenti la superficie del singolo pezzo; la chiamo faccetta per distinguerla dalla faccia del cubo che è costituita da 9 faccette.
Fisicamente la Faccia (face) rappresenta una delle sei superfici piane del cubo; lo Strato (slice) rappresenta invece la stessa faccia vista tridimensionalmente, con anche un'altezza pari all'altezza di un pezzo; in pratica uno strato è uno qualunque dei nove elementi che noi possiamo far girare e che, semplificando (e sbagliando), chiamiamo faccia (nove elementi contando i sei strati associati alle sei facce del cubo ed anche i tre strati intermedi definiti lungo le tre direzioni spaziali).
Naturalmente anch'io dico spesso "ruota la faccia", mentre dovrei dire "ruota lo strato", ma evidentemente è lo stesso perchè non è fisicamente possibile muovere la faccia senza muovere in realtà l'intero strato.
Sistema di riferimento
Le sei faccette centrali determinano il colore di ogni faccia del cubo; cioè ad esempio la faccia arancione (o meglio quella che è la faccia arancione quando il cubo è risolto) è esattamente la faccia dove si vede la faccetta centrale arancione.Le faccette centrali mantengono sempre la loro mutua (reciproca) posizione, cioè per esempio opposta alla faccia centrale bianca ci sarà sempre la gialla, (o quella che è nel vostro cubo la faccia centrale opposta alla bianca).
Le faccette centrali generano per così dire il sistema di riferimento del cubo, che è immutabile;
in pratica per ogni data faccia centrale si avrà sempre lo stesso colore per la faccia centrale opposta
Noi andremo quindi a posizionare ed orientare gli altri pezzi (spigoli ed angoli) in accordo proprio con le faccette centrali che definiscono il colore di ogni faccia.
Colori
Per le sei facce si utilizzano i seguenti colori (le coppie di colori sono su faccette centrali opposte):(Bianco, Giallo)
(Arancio, Rosso)
(Blu, Verde)
Le tre coppie sono disposte in modo che per esempio i tre colori (Bianco, Blu, Arancio) siano disposti secondo una terna levogira.
Nota che ci si potrebbe riferire a una qualunque delle possibili terne levogire di colori (tre colori che si riferiscano a tre facce che abbiano un angolo in comune); esistono 8 angoli e quindi 8 possibili terne levogire di colori che portano tutte a definire univocamente il medesimo identico sistema di colori.
Definizione di Terna levogira
Terna levogira significa che "gira verso sinistra"; cioè associando alle tre facce Bianca, Blu e Arancio nell'ordine i tre assi x, y e z, questa terna ordinata di assi (x, y, z) (ordinata significa che è rilevante l'ordine con cui vengono definiti i tre elementi) si dice levogira se ponendosi in un punto di osservazione definito dalla direzione positiva dell'asse z si osserva il lato positivo dell'asse x sovrapporsi al lato positivo dell'asse y compiendo una rotazione di 90 gradi antiorari.
Invertendo una qualunque delle tre coppie di colori sopra definite si ricade in una terna destrogira.
Notazioni Utilizzate
Notazioni definite dalla WCA (World Cube Association)
(vedi anche WCA notation - notazione articolo 12)
Nei riquadri riporto la traduzione dei vari punti dell'articolo 12.
Mi sono così reso conto che intendevo M e E in versi contrari a quelli ufficiali (vedi mosse dello strato intermedio) e ho quindi adeguato la notazione che uso; in pratica ho semplicemente cambiato in tutte le formule M con M' ed E con E' e viceversa; non capisco però il perché di questa strana scelta da parte della WCA; in particolare non comprendo perché scegliere come versi positivi delle rotazioni degli strati Middle L, D e F quando i tre assi di riferimento sono definiti su R U e F.
Utilizzavo l'altra notazione da sempre e non riesco ad adattarmi alla notazione ufficiale facendo continuamente confusione... forse comincio a spiegarmi perché sia così poco utilizzata e viene piuttosto espressa in altre forme quali Rw R'; preferisco utilizzare l'espressione con M piuttosto che la forma in Rw R' perché risulta molto più leggibile; purtroppo non posso neanche utilizzare la notazione con r, in quanto verrebbe confusa con Rw e non pensata come M (vedi appresso inner slice moves); assolutamente non mi piace questa scelta dei versi di rotazione positivi per gli strati interni M ed E ma purtroppo rimanendo nella notazione ufficiale non vedo alternative.
Le notazioni utilizzate per indicare le sei facce del cubo sono:
- Up or upper face = (faccia in alto)
- Down or bottom face = (opposta alla Up) (faccia in basso)
- Left face = (faccia a sinistra)
- Right face = (faccia a destra)
- Front face = (faccia davanti)
- Back face = (opposta alla Front) (faccia dietro)
Mosse della Faccia (Face Moves)
- Una rotazione di 90 gradi oraria di una faccia, diciamo della faccia U, si indica con U (con l'iniziale del nome della faccia)
- Una rotazione di 90 gradi antioraria di una faccia si indica con l'aggiunta di un apice: U'
- Una rotazione di 180 gradi si indica con l'aggiunta di un 2: U2
- Una rotazione di 180 gradi eseguita in verso antiorario si indica con l'aggiunta di un '2: U'2
evidentemente U2 = U'2 e l'indicazione dell'apice ha il solo scopo di suggerire il verso in cui ruotare la faccia (secondo la particolare tecnica utilizzata di chi descrive la formula)
- 12a1) In verso orario, 90 gradi: F (faccia front), B (faccia back), R (faccia right), L (faccia left), U (faccia upper), D (faccia bottom).
- 12a2) In verso anti orario, 90 gradi: F', B', R', L', U', D' (vedi 12a1).
- 12a3) In verso orario, 180 gradi: F2, B2, R2, L2, U2, D2 (vedi 12a1).
- 12a4) In verso anti orario, 180 gradi: F'2, B'2, R'2, L'2, U'2, D'2 (vedi 12a1).
Il verso orario o antiorario viene stabilito osservando la faccia dall'alto della stessa; cioe' per osservare il lato back gira il cubo in modo da guardare il Back e determina il verso orario od antiorario.
Potresti anche mantenere il cubo fermo e cercare di guardare dietro sporgendo la testa di lato, ma probabilmente è più comodo girare il cubo ;)
È fondamentale apprendere il concetto di rotazione oraria ed anti oraria per ogni faccia, ed applicarla senza sbagliare!
Mosse del doppio strato esterno (Double Outer Slice Moves)
Strato esterno più lo strato interno adiacente (notazione estesa ai 4X4X4) (outer slice plus adjacent inner slice)Viene utilizzata questa notazione per indicare la rotazione di una faccia contemporaneamente alla rotazione dello strato intermedio parallelo a tale faccia (in pratica vengono ruotati due strati e resta fermo solo il terzo).
Si indica la faccia con la maiuscola seguita da w (with - ad indicare che alla mossa della faccia è associata la mossa del corrispondente strato intermedio) (Uw, Lw, Rw, Bw, Rw', Bw2, .... ); l'eventuale apice ' (per -90°) o il 2 (per 180°) vengono aggiunti dopo la w e valgono contemporaneamente per la faccia indicata e per lo strato intermedio ad essa univocamente associato.
- 12a5) verso orario, 90 gradi: Fw, Bw, Rw, Lw, Uw, Dw. (vedi 12a1).
- 12a6) verso antiorario, 90 gradi: Fw', Bw', Rw', Lw', Uw', Dw' (vedi 12a5).
- 12a7) verso orario, 180 gradi: Fw2, Bw2, Rw2, Lw2, Uw2, Dw2 (vedi 12a5).
- 12a8) verso antiorario, 180 gradi: Fw'2, Bw'2, Rw'2, Lw'2, Uw'2, Dw'2 (vedi 12a5).
Fw = F S
Bw = B S'
Rw = R M'
Lw = L M
Uw = U E'
Dw = D E
Come esercizio verifica che
Lw' = R' x = x R' = M' L' = L' M'
Rw = L x = x L = M' R
M = Rw' R
M' = Rw R'
In molti siti è possibile trovare la mossa di un doppio strato definita precedentemente espressa con le stesse lettere utilizzate per la rotazione della faccia, ma in minuscolo (u, l , r, b, r', b2, f'...).
In effetti questa notazione nel sito della WCA viene invece descritta come:
Mosse del solo strato interno
Inner Slice Moves (adjacent slice of outer slice only.- 12a9) verso orario, 90 gradi: f, b, r, l, u, d (vedi 12a1).
- 12a10) verso antiorario, 90 gradi: f', b', r', l', u', d' (vedi 12a9).
- 12a11) verso orario, 180 gradi: f2, b2, r2, l2, u2, d2 (vedi 12a9).
- 12a12) verso antiorario, 180 gradi: f2', b2', r2', l2', u2', d2' (vedi 12a9).
Applicando tale definizione al cubo 3X3X3 si otterrebbe una Middle Slice Move, cioé r = M'.
Limitandosi al cubo 3X3X3 non è quindi necessario usare questa ulteriore notazione che diviene invece indispensabile con cubi di dimensioni superiori.
In tutti i siti in cui tale notazione viene utilizzata questa viene intesa come Mossa del doppio strato Esterno, col significato cioé di r = Rw = M' R e non secondo la definizione della WCA.
Ora non posso credere che tutti sbagliano ad utilizzare questa particolare notazione e sarei quindi portato a pensare che non ho capito io; mi limito comunque a non utilizzare questa notazione nel sito, preferendole piuttosto quella con la w definita precedentemente.
Altre Notazioni
Un altro sistema non definito in modo ufficiale dalla WCA ma che ho visto utilizzato sul sito della Fridrich consiste nell'utilizzare il nome della faccia seguito da s minuscolo per Slice e da a minuscolo per Anti Slice; così per esempio:Rs per Right Slice, cioé Rs = R L'
Ra per Right Anti Slice, cioé Ra = R L
La' Per Left antiorario Anti Slice, cioé La' = L' R'
Come esercizio verifica che
Rs = L' R = R L' = M x = x M = Rw' R x = Lw Rw' x2
Ra = L R = R L = Rw x' R = M Rw2 x' = M' x' R2
Mosse dello strato intermedio (Middle Slice Moves)
(Mosse dello strato intermedio nei cubi con un numero dispari di strati, mosse dei due strati intermedi nei cubi con un numero pari di strati) (middle slice of puzzles with odd number of slices, middle two slices of puzzles with even number of slices)- La rotazione dello strato centrale verticale (tra L e R) si indica con M (Middle slice) e se ne stabilisce il verso orario guardandolo da sinistra (stesso verso di Left)
- La rotazione dello strato centrale orizzontale (tra U e D) si indica con E (Equator Slice) e se ne stabilisce il verso orario guardandolo dalla faccia Down (stesso verso di D)
- La rotazione dello strato centrale verticale parallelo alla Front (tra F e B) si indica con S (Standing Slice), e se ne definisce il verso orario guardandolo dalla faccia Front (stesso verso di F)
- 12a13) In verso orario, 90 gradi: M (stesso verso di L), S (stesso verso di F), E (stesso verso di D). (vedi 12a1).
- 12a14) In verso anti orario, 90 gradi: M', S', E' (vedi 12a13).
- 12a15) In verso orario, 180 gradi: M2, S2, E2 (vedi 12a13).
- 12a16) In verso anti orario, 180 gradi: M'2, S'2, E'2 (vedi 12a13).
Nota che la rotazione della fetta centrale equivale alla rotazione contraria delle due facce laterali, ma quando ruota la fetta centrale tra le facce left e right il sistema di riferimento si sposta; usando per esempio M' la Front diventa la nuova Up; quando invece si ruotano nel verso contrario le facce laterali il sistema di riferimento rimane fermo; quando gira una fetta centrale i colori di riferimento delle faccette centrali in parte cambieranno e si continuerà ad eseguire le mosse basandosi sul nuovo riferimento.
M' = x R' L
M = x' R L'
E' = y U' D
E = y' U D'
S' = z F' B
S = z' F B'
Occorre fare attenzione a non confondersi rispetto al verso di rotazione positivo per M ed E; sarebbe infatti naturale pensarlo associato ai tre assi x, y e z (gli assi che definiscono le rotazioni per l'orientamento dell'intero cubo - vedi appresso) e quindi positivo secondo il verso orario visto dalle facce Right, Up e Front, ma è invece associato al verso positivo (orario) di rotazione delle facce Left, Down e Front.
rotazione (orientamento) dell'intero cubo - impugnatura
A volte si utilizza una notazione per indicare il cambio di impugnatura del cubo nel corso dell'esecuzione di una formula; questo comporta il cambiamento del sistema di riferimento; due delle tre faccette centrali tra Front, Up e Right cambieranno posizione, cioé per rotazioni intorno all'asse x vi troverete a proseguire la formula usando un nuovo colore per le facce Up e Front, per rotazioni intorno all'asse y proseguirete la formula con un nuovo colore per le facce Front e Right mentre per rotazioni intorno all'asse z cambierà il colore delle facce Up e Right.Definiamo i tre assi di riferimento:
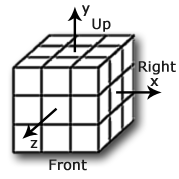
y - perpendicolare alle facce Up e Down, positivo dal lato Up
z - perpendicolare alle facce Front e Back, positivo dal lato Front
con gli stessi simboli si indicano le rotazioni dell'intero cubo per riorientarlo (questo non porta confusione in quanto nelle formule in cui si incontra uno dei simboli x oppure y oppure z non ci si riferisce mai agli assi x, y, z ma alla rotazione da eseguire intorno a tali assi per riorentare il cubo, come descritto nel seguito).
x: rotazione oraria dell'intero cubo di 90 gradi intorno all'asse x |
x = R M' L' |
x': rotazione antioraria dell'intero cubo di -90 gradi intorno all'asse x |
x' = R' M L |
y: rotazione oraria dell'intero cubo di 90 gradi intorno all'asse y |
y = U E' D' |
y': rotazione antioraria dell'intero cubo di -90 gradi intorno all'asse y |
y' = U' E D |
z: rotazione oraria dell'intero cubo di 90 gradi intorno all'asse z |
z = F S B' |
z': rotazione antioraria dell'intero cubo di -90 gradi intorno all'asse z |
z' = F' S' B |
N.B. l'orientamento da dare all'intero cubo e che porta ad una nuova impugnatura va' determinato osservando il cubo dal lato della faccia a cui ci si riferisce e da quel punto di vista si determina la rotazione oraria o antioraria.
Quindi per x o x' si osserva il cubo dalla faccia Right, per y o y' si osserva dalla faccia Up, per z o z' si osserva dalla faccia Front.
Significato delle parentesi nelle formule
Uso le parentesi tonde all'interno delle formule in due situazioni differenti:- Per evidenziare la struttura logica e formale della formula e per facilitarne la lettura, la memorizzazione e la comprensione; individuo tre sotto casi distinti:
- Nel caso ci sia una ripetizione di una sequenza di mosse la scrivo in modo compatto utilizzando il simbolo (...)* e quindi
(espressione) *N
significa che l'espressione in parentesi va' eseguita N volte.
Questo è l'unico caso in cui le parentesi non possono essere ignorate e fanno parte integrante della formula. - Altre volte la utilizzo per evidenziare una mossa di chiusura o di apertura che riposizioni i pezzi (ad esempio nella Niklas posso evidenziare la (U) iniziale che riposiziona correttamente gli angoli), da applicare solo nel caso la strategia utilizzata lo richieda).
- Altre volte le utilizzo per suddividere la formula in parti che - secondo me - hanno una qualche unità logica; tale suddivisione aiuta la memorizzazione della formula; in effetti personalmente eseguendo una formula generalmente la ricordo pensando proprio alla successione di tali blocchi.
A titolo di esempio considerando la formula T Perm:
R U R' U' R' F R2 U' R' U' R U R' F'
sarà molto più semplice memorizzarla come:
(R U R' U') (R' F) (R2 U' R' U' ) (R U R' F')
- Nel caso ci sia una ripetizione di una sequenza di mosse la scrivo in modo compatto utilizzando il simbolo (...)* e quindi
- Per evidenziare una sequenza di mosse che può essere eseguita con un solo movimento della mano (esempio R'U oppure R'F oppure RU') od un solo movimento di entrambe le mani (esempio Lw'UR') e quindi in rapidissima successione.
Il 2 è l'utilizzo che si fa normalmente delle parentesi nei siti che siano orientati verso le risoluzioni veloci (speed solving).
Queste parentesi racchiudono mosse che si alternano in verso orario ed antiorario o viceversa.
Tali tipi di brevi sequenze di mosse sono quasi sempre eseguibili con un unico movimento della mano; mi piace includervi anche le sequenze di mosse eseguibili con un unico movimento di entrambe le mani.
Intuitivamente per unico movimento intendo un movimento congiunto di dita e polso che avvenga senza cambi di direzione.
Tali suddivisioni suggeriscono la modalità di attuazione del movimento da eseguire; con il medesimo intento viene anche a volte indicato U'2 a suggerire l'eventuale verso di rotazione da seguire.
Ovviamente non sono una legge e si potrebbe anche trovare conveniente eseguire altri movimenti.
Per esempio considerando sempre la T Perm vista precedentemente la forma con cui la trovere espressa per lo speed solving è:
R (U R') U' (R' F) (R2 U') R' (U' R) (U R') F'
tale forma suggerisce come eseguirla ma è anche estremamente poco intuitiva e memorizzabile.
Si noti che il posizionamento di tali parentesi nella stragrande maggioranza dei casi è determinabile in modo esatto e non è una invenzione arbitraria di qualcuno.
Un altro aspetto della stessa cosa: avrete sicuramente notato che se una faccia non è perfettamente allineata, eseguendo la mossa successiva alle volte la faccia disallineata si riallinea e a volte invece tale disallineamento blocca la mossa successiva.
eseguita una qualunque mossa la successiva potrà avvenire prima del termine della mossa precedente solo se il verso di rotazione della seconda mossa è opposto al verso di rotazione della prima mossa; al contrario se le due mosse sono entrambe orarie od entrambe antiorarie allora per eseguire la seconda occorrerà terminare completamente la prima ed anzi la seconda mossa potrà essere più facilmente eseguita (senza pericolo di inceppamento) se la prima mossa eccede lievemente la rotazione esatta.
Il fatto che le rotazioni delle facce adiacenti siano contrarie si traduce sui tre blocchetti che sono in comune tra le due facce in un movimento sempre nella stessa direzione e questo fa sì che possa essere eseguito con un solo movimento della mano.
Quindi quando le rotazioni si alternano le due mosse potranno essere eseguite con un unico movimento di una o di entrambe le mani; a questo punto interviene anche la tecnica personale: alcune volte questo sarà molto semplice da fare; due esempi che tutti sarete facilmente in grado di eseguire in un solo movimento sono:
(R U') [il polpastrello del pollice della mano destra esegue le due mosse]
oppure
(R' U) [l'indice della mano destra esegue entrambe le mosse in un sol colpo]
per eseguire invece
R U oppure R' U'
saranno necessari due movimenti.
Altre volte il movimento potrebbe essere meno intuitivo da trovare; per esempio:
(R' F) può essere eseguita con un unico movimento in due modi:
suppongo che teniate il cubo nella posizione di partenza così come lo tengo io:
Per la mano sinistra (che mantiene il cubo) il pollice sulla faccetta centrale Front, medio e anulare sui due strati inferiori della faccia Back, l'indice può eseguire con facilità U'.
il primo modo consiste nel cambiare impugnatura della mano sinistra ed eseguire
(Lw' U) x'
x' serve semplicemente per ripresentare il cubo con l'orientamento che aveva prima dell'esecuzione della sequenza
il secondo modo (molto più rapido) consiste nell'eseguire semplicemente
(R' F) [con l'indice della mano destra]
senza cambiare impugnatura (finger trick); bisogna tenere il pollice della mano sinistra esattamente sulla faccetta centrale, esercitando una pressione leggera, che sia sufficiente a tenere il cubo ma non tale che blocchi la rotazione della front (se il pollice stà poggiato esattamente sul centro è difficile poterla bloccare); può essere utile aiutarsi col mignolo sinistro poggiato sulla faccia Down ad impedire il movimento dello strato centrale S quando si esegue F.
Ad eccezione del caso 1.1 le parentesi vanno sempre considerate come semplici suggerimenti su come eseguire o su come memorizzare gli algoritmi risolutivi.
Individuare una posizione
Possiamo individuare una posizione di un pezzo dandone le coordinate:Angoli
URF - Up Right FrontULF - Up Left Front
URB - Up Right Back
ULB - Up Left Back
DRF - Down Right Front
DLF - Down Left Front
DRB - Down Right Back
DLB - Down Left Back
Spigoli
UF - Up FrontUL - Up Left
UR - Up Right
UB - Up Back
LF - Left Front
LB - Back Left
RF - Right Front
RB - Right Back
DF - Down Front
DL - Down Left
DR - Down Right
DB - Down Back
così per esempio con URF si indica la posizione d'angolo Up Right Front e con BL la posizione Back Left.
Una volta scelta una impugnatura del cubo, cioè scelta una faccia Up ed una faccia Front (la scelta di due facce determina completamente la posizione spaziale del cubo), la notazione si riferisce alla posizione complessiva del cubo (all'impugnatura) ed al pezzo che è in quella posizione in quel momento, non al pezzo che dovrebbe andare lì.
Applicando una formula risolutiva quando decidi che il tuo lato U è, per esempio, il bianco dovrai semplicemente badare a che la faccetta centrale bianca resti sempre in U e che la faccetta di Altro Colore che è in F resti sempre in F (e così per le altre facce centrali ovviamente, ma mantenendo il riferimento su due facce centrali tutto il cubo rimane fissato - ovvero per il posizionamento del sistema di riferimento delle facce centrali esistono 2 gradi di libertà).
Ovviamente non occorre controllare visivamente la faccetta centrale, in quanto si dovrebbe pensare ad altre cose come cercare di posizionare gli altri pezzi nel modo corretto, ma sarà semplicemente il contatto fisico della mano con il cubo (l'impugnatura) a ricordarti in ogni istante il corretto posizionamento consentendoti di mantenere il riferimento; applicando le formule potresti perdere il senso dell'orientamento in quanto per applicare le mosse velocemente devi a volte girare il cubo nelle mani cambiando impugantura; in tale circostanza ti affiderai quindi solo ad una sequenza mnemonica di mosse per eseguire la formula perdendo temporaneamente il senso dell'orientamento; devi solo badare ad eseguire correttamente la formula di cui hai memorizzato la sequenza.
Terminologia utilizzata per lo spostamento dei pezzi
Considerando un singolo pezzo (Spigolo od Angolo) possiamo riscontrare due tipologie di movimento: il pezzo può ruotare su se' stesso (orientamento) oppure spostarsi dalla propria posizione per effetto di una permutazione o mutua rotazione fra diversi pezzi (posizionamento); se lo spostamento implica 2 pezzi si parla di scambio se implica tre (o più) pezzi si parla di permutazione.Orientamento
Considera la rotazione sul posto del pezzo.La rotazione sul posto si riferisce ad entrambi i tipi di pezzi (angoli e spigoli).
ribaltamento è la rotazione di uno spigolo su sé stesso (avendo due sole facce semplicemente si ribalta) parlerò di spin 1/2 = -1/2 se risulta ribaltato e di spin 0 se risulta orientato correttamente
rotazione sul posto è la rotazione su sé stesso di un angolo (con spin 0 se orientato correttamente e spin 1/3 e -1/3 = 2/3 per gli altri due possibili casi)
Parlerò di orientamento quando utilizzerò il concetto di rotazione sul posto per definire la disposizione del cubetto nell' esatto orientamento finale, a prescindere dal posizionamento dello stesso pezzo.
Mentre appare evidente il concetto di orientamento per un pezzo che si trovi nella giusta posizione, appare molto meno immediato pur se possibile definire l'orientamento per un pezzo che non si trovi nella sua corretta posizione finale; in tal caso normalmente si considera l'orientamento di un pezzo non in assoluto ma relativamente ad una delle facce cui appartiene il pezzo stesso (per esempio nel metodo Fridrich si considera l'orientamento dei pezzi dell'ultima faccia relativamente all'ultima faccia stessa).
Posizionamento
Considera lo scambio di posizione di un pezzo con altri pezzi, ovvero la mutua rotazione tra alcuni pezzi ovvero la loro permutazione.La rotazione fra diversi pezzi o mutua rotazione o permutazione si riferisce sia agli spigoli che agli angoli.
scambio (swap) è la mutua rotazione o permutazione di due soli pezzi
mutua rotazione o permutazione (permutation) è la rotazione tra loro di tre o più pezzi dello stesso tipo (angoli o spigoli)
Parlerò di posizionamento intendendo la permutazione tra pezzi (dello stesso tipo) col fine di posizionare i cubetti nella corretta posizione finale (a prescindere dall'orientamento di tali pezzi).
Disposizione
Per disposizione di un pezzo intendo il suo contemporaneo posizionamento ed orientamento.Disporre un pezzo = Posizionare il pezzo nella giusta posizione e con il corretto orientamento.
In particolare, siccome andremo sempre ad eseguire delle formule che coinvolgano il minor numero di pezzi compatibilmente con le leggi fisiche che regolano il movimento dei pezzi nel cubo, il tipo di spostamenti più elementari che potrete osservare saranno:
per il posizionamento:
- lo scambio di due coppie di pezzi
- la permutazione di tre pezzi
- il ribaltamento di due spigoli
- la rotazione su sé stessi con uguale spin di tre angoli
- la rotazione su sé stessi con spin opposti di due angoli
Normalmente il cubo si comincia a costruire completando una prima faccia;
a volte indicherò questa come Prima faccia o First Layer (FL) e la sua opposta come Ultima faccia o Last Layer (LL) o anche mi riferirò al Colore Prima Faccia e Colore Ultima Faccia; farò anche riferimento a volte alle Facce Laterali riferendomi alle 4 facce comprese tra la prima faccia e l'ultima.
