Metodo a strati Fridrich semplificato
Premessa
Il metodo Fridrich semplificato consente di risolvere il cubo seguendo la metodologia utilizzata nel Fridrich completo ma utilizzando un set limitato di formule scelte tra quelle utilizzate nel metodo completo; con questo metodo semplificato si può arrivare a risolvere il cubo in meno di 30 secondi (imparando anche un F2L per i primi due strati).
Successivamente potrete gradualmente integrare questo metodo semplificato con tutte le restanti formule del metodo completo.
Nel Passo 2 di orientamento degli angoli ho scelto di utilizzare alcune formule tra quelle proposte da Lars Petrus nel suo metodo ed ho tratto i nomi delle formule dal suo sito.
Questo metodo consente di risolvere il terzo strato in 4-look, ossia ognuno dei 4 passi verrà eseguito una sola volta.
Se siete alle prime armi potete imparare dapprima il metodo semplificato principianti e successivamente integrarlo con il metodo intermedio spiegato in questa pagina, cioé potrete continuare ad utilizzare le formule già apprese nel metodo per principianti aggiungendo le nuove formule del metodo intermedio via via che le imparate.
Esistono numerosi siti dove trovare la lista di formule per il Metodo Fridrich completo; nota che in generale ognuno usa un set lievemente diverso di formule.
OLL
Jessica Fridrich Site
Jon's Rubik's Cube Page
Macky's Cube Freak
Lars Vandenbergh's CubeZone
Joël van Noort - Solve the Cube
Bob Burton - Cubewhiz
PLL
Jessica Fridrich Site
Jon's Rubik's Cube Page
Macky's Cube Freak
Lars Vandenbergh's CubeZone
Joël van Noort - Solve the Cube
Bob Burton - Cubewhiz
Metodo Semplificato
Riguardo al Fridrich semplificato esistono diversi video in italiano su YouTube; voglio segnalare per la sua completezza e chiarezza quello di
zyky2000 OLL
zyky2000 PLL part 1
zyky2000 PLL part 2
Il metodo che descrivo in questa pagina è analogo al metodo Fridrich Semplificato ottimamente spiegato nei video di Zyky, solo usando qua e là altre formule o differenti espressioni per le stesse formule (traslate, simmetriche o inverse); possono rivelarsi molto utili i suggerimenti che Zyky da' su come individuare velocemente una configurazione specie se impiegate più tempo a decidere quale formula eseguire piuttosto che ad eseguirla effettivamente.
Il metodo utilizza complessivamente 19 formule:
10 per l’OLL semplificato
9 per il PLL semplificato
Notazione
È ovviamente assolutamente necessario imparare quelle poche nozioni necessarie per leggere ed interpretare correttamente le formule; nel caso aveste dei dubbi consultate la pagina delle notazioni.Il Fridrich Semplificato si esegue in 6 passi:
- Croce iniziale - posizionamento ed orientamento dei 4 spigoli della prima faccia
- F2L (First Two Layers) - posizionamento ed orientamento di ogni angolo del primo strato assieme al corrispondente spigolo del secondo strato in 4 looks (uno per ogni slot).
- EOLL (Edges Orient Last Layer) orientamento spigoli ultimo strato
[3 Formule - max 12 mosse] - COLL (Corners Orient Last Layer) orientamento angoli ultimo strato
(7 Formule - dal metodo Lars Petrus) [max 11 mosse] - CPLL (Corners Permute Last Layer) posizionamento angoli ultimo strato
(5 Formule) [max 12 mosse] - EPLL (Edges Permute Last Layer) posizionamento spigoli ultimo strato
(4 Formule) [max 14 mosse]
Primo e Secondo strato
La risoluzione del primo e secondo strato è separata ed indipendente dalla risoluzione del terzo (ultimo) strato.È opportuno utilizzare una tecnica F2L in due passi descritta in altra pagina.
Terzo Strato
Da ora in avanti la faccia che resta da risolvere sarà la nostra faccia U.Nella risoluzione che propongo indico in neretto come prima formula quella che è la mia "prima scelta", dando a volte delle possibili alternative che mi piacciono; in tali forme alternative quando necessario utilizzo all’inizio della formula y o y2 o y' per riorientare il cubo prima di applicare l'algoritmo in modo da utilizzare un’unica figura per descrivere lo configurazione in questione; infatti ogni figura si riferisce comunque sempre alla prima formula evidenziata in neretto.
A volte per una data formula posso anche indicare una diversa espressione equivalente (quando utilizzo il segno =).
Le parentesi evidenziano delle mosse che si possano eseguire con un unico movimento di una o di entrambe le mani o a volte anche un doppio movimento comunque eseguibile in rapidissima successione; vedi uso delle parentesi negli algoritmi.
Nelle figure:
giallo: colore dell’ultima faccia
bianco: faccette ordinate di colore imprecisato
grigio chiaro: faccette ancora da ordinare di colore imprecisato
grigio scuro: posizioni in fase di ordinamento (interessate dalla formula in esame) di colore imprecisato
il giallo è usato in luogo di uno degli altri tre colori qualora sia possibile definirlo con certezza
Passo 1 - EOLL (Edges Orient Last Layer) - Forma la croce dell’ultimo strato (orienta gli spigoli)
In questo passo si orientano gli spigoli osservando solo il loro lato sulla faccia U e prescindendo dal loro corretto posizionamento; cioè dobbiamo fare in modo di avere i colori degli spigoli sulla faccia Up tutti dello stesso colore della faccetta centrale Up senza occuparci del secondo colore di ogni spigolo.Si possono avere le seguenti situazioni:
-
1.1
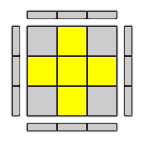
I quattro spigoli sono orientati tutti correttamente il loro colore sulla faccia U corrisponde al colore della faccetta centrale su U: non fare nulla, la croce è già fatta.
- vai al passo 2
-
1.2
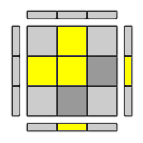
Due spigoli adiacenti risultano ribaltati e gli altri 2 corretti. posiziona il cubo in modo che i 2 spigoli orientati correttamente siano in posizione UL e UB e i due spigoli ribaltati siano in posizione UF e UR e applica la formula:
- x (U R') (U' Lw) U (R U') R'
oppure
F U R U' R' F' - Vai al passo 2
- x (U R') (U' Lw) U (R U') R'
-
1.3
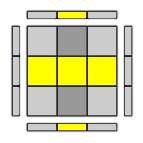
Due soli spigoli in posizione opposta risultano ribaltati.
Posiziona il cubo in modo che i due spigoli orientati correttamente siano in posizione UL e UR e i 2 spigoli ribaltati in posizione UF e UB. Applica:- R (U R') U' (R' F) (R F') = R (U R') U' (Lw' U) (R U') x' (inversa della precedente)
oppure:
F R U R' U' F' (inversa della alternativa precedente) - Vai al passo 2
- R (U R') U' (R' F) (R F') = R (U R') U' (Lw' U) (R U') x' (inversa della precedente)
-
1.4
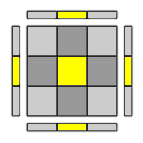
I quattro spigoli risultano tutti ribaltati.
Mantenedo sempre in Up l’Ultima Faccia e con una qualunque scelta per la faccia Front applica- Rw' R U R (U R') U' Rw2 (R2' U) (R U') Rw' = M U R (U R') U' M2 U (R U') Rw'
- vai al passo 2
Passo 2 - COLL (Corners Orient Last Layer) - Orienta gli angoli dell’ultimo strato
-
2.1

I quattro angoli sono tutti orientati correttamente: non occorre fare nulla.
- vai al passo 3
-
2.2

Un solo angolo è orientato correttamente; gli altri tre risulteranno ruotati con spin -1/3.
Posiziona il cubo mantenedo l’angolo orientato correttamente in ULF ed applica la formula:- (Sune) R (U R' U) (R U2) R'
(Niklas) R U' L' U R' U' L - vai al passo 3
- (Sune) R (U R' U) (R U2) R'
-
2.3

Se gli altri tre risulteranno ruotati con spin +1/3 posiziona il cubo mantenedo l’angolo orientato correttamente in ULB ed applica:
- (Sune Simmetrica) R' (U' R U') (R' U2) R
(Anti Sune - Sune Inversa) y R U2 R' U' R U' R'
(Niklas simmetrica) y2 L' U R U' L U R' - vai al passo 3
- (Sune Simmetrica) R' (U' R U') (R' U2) R
-
2.4

Due angoli sono orientati male (con spin opposti) mentre gli altri due sono orientati correttamente; esistono tre possibili configurazioni.
Prima possibilità:- (Perfect Sequence Dx) Lw2 (U R') D2 (R U') R' D2 Lw' x = R2 D R' U2 R D' R' U2 R'
(Denzel) y x' U2 R2 U' L2 U R2 U' L2 U' x - vai al passo 3
- (Perfect Sequence Dx) Lw2 (U R') D2 (R U') R' D2 Lw' x = R2 D R' U2 R D' R' U2 R'
-
2.5

Due angoli sono orientati male. Seconda possibilità:
- (Evelyn inversa) Rw (U R') U' L' U (R U') x' = x L U R' U' L' U R U' x'
- vai al passo 3
-
2.6

Due angoli sono orientati male. Terza possibilità:
- (Evelyn) x (U R') (U' L) U (R U') Rw' = x U R' U' L U R U' L' x'
(Triple Sune) y2 R (U R' U) (R U') (R' U) (R U') (R' U) (R U2) R' - vai al passo 3
- (Evelyn) x (U R') (U' L) U (R U') Rw' = x U R' U' L U R U' L' x'
-
2.7

I quattro angoli sono tutti orientati male; due con spin +1/3 e due con spin -1/3 ; esistono due sole configurazioni possibili a cui ricondursi. Prima possibilità:
- (Double Sune) R (U R' U) (R U') (R' U) (R U2) R'
- vai al passo 3
-
2.8

Quattro angoli tutti orientati male.
Seconda possibilità:- (Bruno) R U2 R2 U' R2 U' R2 U2 R
- vai al passo 3
Passo 3 - CPLL (Corners Permute Last Layer) - Posiziona gli angoli dell’ultimo strato
Si tratta ora di disporre correttamente i 4 angoli sulla faccia U cioé metterli nella giusta posizione senza alterare l’orientamento già ottenuto nei passi precedenti.Metti nella giusta posizione il maggior numero possibile di pezzi (spigoli ed angoli) adiacenti (contigui) ruotando opportunamente la faccia Up.
Potrebbero non esserci pezzi contigui da mettere in posizione corretta, nel qual caso semplicemente posiziona correttamente il maggior numero di pezzi, che saranno o 4 angoli o 4 spigoli.
A seconda della configurazione (stato) che trovi esegui uno dei seguenti passi:
-
3.1

I quattro angoli sono tutti nella posizione corretta; non occorre fare nulla.
- Vai al passo 4
-
3.2

Un solo angolo è nella posizione corretta: occorre permutare gli altri tre angoli. Se devono ruotare in senso antiorario posiziona l’angolo corretto in ULB e applica la formula:
- (Lw U' R) D2 (R' U) R D2 R2 x
- Vai al passo 4
-
3.3

Un solo angolo è nella posizione corretta; se gli altri tre devono ruotare in senso orario posiziona il cubo mantenendo l’angolo corretto in ULF e usa la formula:
- (Lw' U R') D2 (R U') R' D2 R2 x' (simmetrica della precedente)
- Vai al passo 4
-
3.4

Due angoli adiacenti sono scambiati tra loro e gli altri due sono disposti correttamente. Orienta il cubo mantenendo i due angoli da scambiare in URF e URB e applica la formula:
- (J Perm) R (U R') (F' R) (U R') U' (R' F) (R2 U') R' U'
(T Perm) R (U R') U' (R' F) (R2 U') R' (U' R) (U R') F' - Vai al passo 4
- (J Perm) R (U R') (F' R) (U R') U' (R' F) (R2 U') R' U'
-
3.5

Due angoli sulla diagonale (opposti) sono scambiati tra loro e gli altri due sono disposti correttamente.
Orienta il cubo mantenendo i due angoli da scambiare in ULF e URBe applica la formula:- (Y Perm) F (R U') R' (U' R) (U R') (F' R) (U R') U' (R' F) (R F')
R2 U R2 U R2 y U' R' U' Lw D2 Lw' U R - Vai al passo 4
- (Y Perm) F (R U') R' (U' R) (U R') (F' R) (U R') U' (R' F) (R F')
-
3.6

Due coppie di angoli adiacenti sono scambiate tra loro. In tal caso i quattro spigoli si troveranno già nella giusta posizione. Orienta il cubo come da figura e applica la formula:
- x (U R') (U' L) U (R U') Rw'2 (U' R) U (L U') (R' U) x
- Vai al passo 4.1
-
3.7

Due coppie di angoli opposti (sulla diagonale) sono scambiate tra loro. In tal caso i quattro spigoli si troveranno già nella giusta posizione. Applica:
- U2
- Vai al passo 4.4
Passo 4 - EPLL (Edges Permute Last Layer) - Posiziona gli spigoli dell’ultimo strato
-
4.1

Se gli spigoli sono tutti nelle loro posizioni corrette:
- Finito
-
4.2

Un solo spigolo è in posizione corretta allora occorrerà far ruotare tra loro (permutare) gli altri tre spigoli. se i rimanenti tre devono ruotare mutuamente (permutare) in senso orario posiziona il cubo in modo che lo spigolo corretto si trovi in UB e applica la formula:
- (Allan) F2 U M' U2 M U F2
y2 (R' U) R' U' R' U' (R' U) R U R2 - Finito
- (Allan) F2 U M' U2 M U F2
-
4.3

Un solo spigolo è in posizione corretta e gli altri tre devono invece ruotare mutuamente (permutare) in senso antiorario.
Posiziona lo spigolo corretto in UB e applica la formula:- (Allan simmetrica) F2 U' M' U2 M U' F2
y2 (R2 U') R' (U' R) U R U (R U') R - Finito
- (Allan simmetrica) F2 U' M' U2 M U' F2
-
4.4

Scambio di due coppie di spigoli opposti (in asse con la faccetta centrale).
Mantenedo sempre in Up l’Ultima Faccia e per una qualunque scelta della faccia Front applica:- M2 U M2 U2 M2 U M2
Ra U2 Ra' Fa' U2 Fa (Fridrich)
R2 Bs2 L2 D' R2 Bs2 L2 (U) (Fridrich) - Finito
- M2 U M2 U2 M2 U M2
-
4.5

Scambio di due coppie di spigoli adiacenti. Posiziona il cubo in modo da avere le due coppie da scambiare in (UF, UL) e (UR, UB) ed applica:
- M2 U M' U2 M2 U2 M' U' M2
Ls Ds2 Ls D Ls2 U' Bs2 (Fridrich)
R' F R Ba' R Fs R F'R'B2 (U') (Fridrich)
y x' (R U') (R' U) D R' D U' (R' U) R D2 x U (jon) - Finito
- M2 U M' U2 M2 U2 M' U' M2
