Formule per la Risoluzione del cubo magico
Introduzione
Formule di risoluzione
Definizione:Una Formula risolutiva del cubo magico è una sequenza di mosse che consenta di spostare (posizionare e/o orientare) solo pochi pezzi del cubo (spigoli e/o angoli) mantenendo inalterata la posizione e l'orientamento di tutti gli altri pezzi.
Nel seguito mi riferirò a formule che consentano di spostare alcuni pezzi dell'ultimo strato di un ipotetico metodo a strati; non considero quindi eventuali formule da applicare su pezzi che non si trovino tutti sull'ultimo strato.
I parametri che definiscono la "potenza di una formula" potrebbero essere:
- Il numero di mosse che la formula richiede: meno mosse la formula utilizza e meglio è
- Il numero di pezzi coinvolti: meno pezzi coinvolge più è potente
- la facilità di memorizzazione
- la naturalezza e quindi la rapidità della sua esecuzione
Il set di formule proposto da Lars Petrus e i set di formule utilizzati nel metodo Fridrich.
Alcune di queste sono anche nelle tabelle di questa pagina.
Voglio inoltre segnalare il sito di Bernard Helmstetter che tramite un programma ha trovato una lista di formule (lui spiega di aver ricercato tutte le formule fino a 15 mosse di lunghezza più una parte di quelle di lunghezza 16) praticamente per ogni possibile configurazione dell'ultimo strato (analizza qualcosa come 1212 configurazioni differenti).
Quindi occorre semplicemente definire uno schema di risoluzione e trovare un semplice set di formule da utilizzare per eseguire il metodo scelto.
Nel seguito della pagina nelle prime tre tabelle ho raccolto un elenco base di formule per risolvere il cubo piuttosto note e caratterizzate dall'essere le più semplici da apprendere in quanto sono tutte piuttosto brevi e richiedono movimenti delle mani abbastanza naturali; utilizzando alcune di queste (nei metodi a strati per principianti se ne usano in genere 4) è possibile risolvere il cubo utilizzando diversi semplici metodi risolutivi.
Mosse Atomiche
Riferendosi alle leggi del cubo magico si capisce che gli spostamenti dei pezzi provocati da una qualunque formula sono comunque riconducibili ad una concatenazione (successione) di qualcuna delle seguenti tipologie di spostamenti elementari:- scambio di due coppie di spigoli (posizionamento) (swapping edges)
- scambio di due coppie di angoli (posizionamento) (swapping corners )
- scambio di una coppia di spigoli e di una coppia di angoli (posizionamento) (swapping edges and corners)
- orientamento (ribaltamento)(flipping) (rotazione sul posto) di due spigoli (orienting edges)
- orientamento (rotazione sul posto) con versi contrari di due angoli (orienting corners)
- orientamento (rotazione sul posto) con uguale verso di tre angoli (orienting corners)
- permutazione (mutua rotazione) tra tre spigoli (posizionamento) (permuting edges)
- permutazione (mutua rotazione) tra tre angoli (posizionamento) (permuting corners)
Queste sono le Mosse Atomiche imposte dalla fisica del cubo ai pezzi componenti il puzzle nel senso che
non esistono spostamenti più semplici; sono cioè i movimenti base o elementari dei pezzi del cubo.
In pratica non puoi semplicemente scambiare di posto due pezzi, senza che anche un'altra coppia di pezzi si scambi, e non puoi ruotare un pezzo su sé stesso (orientare) senza che anche qualche altro pezzo delle stesso tipo pure ruoti in modo che la somma degli spin di tutti i pezzi dello stesso tipo dia sempre 0 o un intero con segno (0 modulo 1).
Lo Spin è la rotazione su sé stesso (orientamento) di un pezzo.
L'angolo può avere spin 0 o +1/3 o -1/3 = 2/3.
Lo spigolo può avere spin 0 o +1/2 = -1/2.
Utilizzando in sequenza alcuni di questi spostamenti elementari o atomici (quali dipende ovviamente dalla particolare configurazione da risolvere) si può quindi arrivare a completare l'ultima faccia.
Ogni possibile configurazione dell'ultimo strato che si voglia risolvere e quindi ogni formula che risolva (direttamente) tale problema è sempre riconducibile ad una qualche concatenazione (successione) delle mosse atomiche sopra elencate.
Ovviamente non siete costretti a risolvere la faccia utilizzando una sequenza di mosse elementari, ma potreste usare una formula che la risolva direttamente, solo che il numero di formule da conoscere in tal caso passa da quelle poche che definiscono le mosse elementari a parecchie decine di formule e diviene un metodo per esperti.
Si nota anche che non è possibile definire una semplice permutazione di 4 pezzi così come fatto per la permutazione di 3 pezzi
in pratica la permutazione di 4 pezzi (4-cycle perm) si comporta come un singolo scambio di due pezzi, cioé per ottenere una permutazione di 4 pezzi (angoli o spigoli) occorrerà contemporaneamente (limitandosi a considerare spostamenti di pezzi sull'ultimo strato) avere sull'altro tipo di pezzi (spigoli o angoli) o una permutazione di 4 pezzi in verso contrario o il secondo scambio semplice di due pezzi o una permutazione di 4 pezzi incrociata ("a clessidra") onde soddisfare la legge dello scambio dei pezzi.
Le stesse mosse atomiche che ho indicato sono in effetti ridondanti: per esempio potete ottenere uno scambio tra due coppie di spigoli applicando due volte (posizionando opportunamente il cubo prima di applicare ognuna delle due formule) una permutazione tra tre spigoli, e quindi uno scambio di due coppie non è una mossa atomica ma è riconducibile a una doppia permutazione tra tre pezzi e viceversa la mutua rotazione tra tre pezzi è riconducibile ad un doppio scambio di due coppie.
Il fatto che esista uno scambio misto di due coppie di pezzi non riproducibile da una permutazione di tre pezzi mi fa' ritenere che le vere mosse atomiche originarie siano lo scambio e l'orientamento, mentre la permutazione di tre pezzi è ottenuta da un doppio scambio; siccome risolvendo l'ultima faccia si deve tipicamente risolvere o uno scambio di due coppie oppure la permutazione di angoli e/o spigoli, mi piace esporre la cosa definendo sia la permutazione tra tre pezzi che lo scambio tra due coppie come mosse atomiche.
Qualunque altro spostamento - formula è ottenibile tramite una successione (concatenazione) di queste sole mosse atomiche.
Qualunque configurazione del cubo è ottenibile utilizzando una sequenza di queste sole mosse atomiche e viceversa, partendo da una qualunque configurazione iniziale è possibile risolvere il cubo utilizzando solo queste mosse atomiche per muovere i pezzi.
Per ognuna delle mosse atomiche esistono numerose formule possibili conosciute o forse non ancora scoperte o divulgate, anche se in effetti per le formule che coinvolgono 3 o 4 pezzi è assai improbabile che ci siano formule equivalenti a quelle note ancora da scoprire che richiedano un minor numero di mosse per essere eseguite.
Ovviamente ogni formula può essere traslata in modo da utilizzare altre facce nell'eseguirla.
Si potrebbe anche pensare di usare le formule al contrario (formula inversa) per ottenere un movimento dei pezzi (permutazione e rotazione) in verso contrario oppure una formula simmetrica per ottenere lo stesso risultato; personalmente ho deciso di adottare per alcune formule le inverse e per altre le simmetriche, come si vede nelle tavole.
Ciclicità delle formule
Tutte le formule hanno una natura ciclica: applicando più volte la stessa formula, questa riporterà il cubo nella configurazione che si aveva inizialmente; il numero di volte che è necessario applicarla prima di tornare alla configurazione iniziale varia con la formula.Più in generale si osservi che
Per una qualunque arbitraria sequenza di mosse scelta in modo completamente arbitrario e con una qualunque lunghezza, esiste un numero N tale che eseguendo la sequenza N volte (N che varia per ogni sequenza scelta) si ritorna alla configurazione di partenza.
Tale numero N per la maggior parte delle sequenze di mosse che esistono è un numero elevatissimo (centinaia o migliaia di mosse o anche più) e le formule risolutive propriamente dette sicuramente godono della proprietà di tornare alla configurazione iniziale eseguendo un piccolo numero di iterazioni della sequenza.
Normalmente le formule hanno ciclicità 2 o 3 ma esistono formule (utilizzate effettivamente in qualche metodo) che hanno ciclicità superiore, quali 5 o 6 o anche 12 (ad esempio la "Rurubub" ha ciclicità 12 e la "Sune" ha ciclicità 6); al contrario per esempio la sequenza U R (che è una semplice sequenza di mosse ma non è una formula) ha ciclo 106.
Le prime formule a cui saremmo interessati sono quelle sequenze che realizzano le mosse atomiche ossia i più semplici spostamenti di pezzi realizzabili nel cubo; vedrete però che spesso si preferisce usare formule che spostano un maggior numero di pezzi ma che risultano più brevi da eseguire.
Orientamento e Permutazione
Come osservato i movimenti atomici sono fondamentalmente di due tipi: orientamento e posizionamento (permutazione e scambio) (per posizionamento intendo quindi la sola dislocazione spaziale, prescindendo dall'orientamento del pezzo).Si osserva che una formula può essere solo di orientamento o solo di posizionamento o può eseguire entrambe le tipologie di spostamenti; inoltre una formula può agire solo sugli angoli o solo sugli spigoli o su entrambi.
Quale utilizzare sarà dettato dal tipo di strategia di risoluzione adottata.
Formula Inversa
La formula inversa di una data formula si ottiene eseguendo tutte le mosse della formula di partenza (formula diretta) partendo dall'ultima mossa e arrivando alla prima ed eseguendo tutte le mosse nel verso contrario.Dando un esempio l'inversa di R' U' R U B' U' B' è B U B' U' R' U R .
Questo porta ad una formula che esegue lo stesso lavoro di quella di partenza permutando e orientando tutti gli stessi pezzi coinvolti dalla formula diretta ma in verso contrario.
Così come per una singola mossa, per esempio R per la mossa Right, la rotazione contraria, R', è la sua inversa e viene indicata con l'apice, anche per una formula X se ne definisce l'inversa con l'aggiunta di un apice: X'.
Formalmente:
dette ad esempio a,b,c,d una successione di 4 generiche mosse eseguite sul cubo (e ognuna possa essere oraria o antioraria, cioé l'apice sia inglobato nella lettera minuscola stessa) e definita X la sequenza ordinata
X = (a b c d)
allora chiameremo inversa della sequenza X, e la indicheremo con X':
X' = (a b c d)' = (d' c' b' a')
Si noti che definire quale delle due sia la diretta e quale l'inversa è una scelta puramente arbitraria.
In pratica trovi una formula e decidi di chiamare quella come diretta e l'altra sarà allora l'inversa.
Si noti che data una qualunque formula è sempre possibile definirne l'inversa.
La fondamentale caratteristica della formula inversa di una data formula è che se eseguita in successione alla formula di partenza riporta il cubo nella condizione iniziale precedente all'applicazione della formula stessa.
formalmente:
X X' = Identità
Dove la funzione Identità (brevemente I) non esegue alcuna operazione.
Si noti anche che eseguendo prima l'inversa e poi la diretta il risultato è lo stesso (del resto quale sia diretta e quale sia inversa è arbitrario)
X' X = Identità
In genere l'apprendimento dell'inversa (o della simmetrica - riflessa) di una formula già imparata è molto rapido.
Chiaramente in formule con ciclicità 2 non serve imparare l'inversa in quanto è identica alla diretta; è invece di solito utile in tutte le formule con ciclicità maggiore o uguale a tre, dove per ottenere lo stesso risultato dell'inversa occorrerebbe applicare la diretta N-1 volte, se N è la ciclicità della formula.
Formula Inversa = (Formula Diretta) * (N-1)
essendo N la ciclicità della formula.
dimostrazione:
Sappiamo che eseguendo per N volte una formula di ciclo N si ritorna alla configurazione di partenza.
Quindi se la eseguiamo N-1 volte sappiamo che eseguendola un'ulteriore volta torneremo al punto di partenza.
Sappiamo anche che se eseguiamo la formula inversa e immediatamente dopo la sua diretta ancora torniamo nella situazione di partenza.
Cioè
N-1 volte diretta + 1 volta diretta = 1 volta inversa + 1 volta diretta = Identità
Quindi vuol dire che se eseguiamo N-1 volte la diretta ci poniamo nella stessa situazione (nella stessa configurazione) che se eseguissimo una sola volta l'inversa.
L'inversa di una Formula viene anche chiamata col nome della Formula stessa preceduto da anti:
(Nome_Formula) Inversa = Anti (Nome_Formula).
Formula Simmetrica - Riflessa
La formula simmetrica o riflessa ha la stessa funzione della inversa anche se le due forme possono dare risultati "secondari" lievemente differenti; per esempio nella Sune utilizzata per orientare gli angoli la Sune simmetrica e la Sune inversa (la Anti Sune) danno lo stesso risultato primario riguardo l'orientamento degli angoli ma come effetto secondario danno differenti permutazioni per gli spigoli; nel caso non ci siano effetti secondari indesiderati la decisione di usare la simmetrica o l'inversa dipende solo da preferenze personali.Mentre l'inversa ha lo stesso comportamento della formula diretta, per cui applicando la diretta e poi la inversa si ritorna esattamente alla situazione di partenza, utilizzando una simmetrica, a causa dei possibili effetti secondari diversi, in generale non si tornerà alla configurazione di partenza, in quanto potranno permanere gli effetti secondari.
Parlo di simmetria in generale ma in effetti si dovrebbe definire rispetto a quali piani avviene tale simmetria; nella stragrande maggioranza dei casi la simmetria si definisce rispetto ad uno dei piani definiti da due dei tre assi x,y e z, ( di solito rispetto al piano che passa per gli assi y e z) ma si potrebbero considerare altri piani di simmetria; per esempio nella rurubub il piano di simmetria della buburur è definito come il piano che passa per l'asse y (quindi perpendicolare alla faccia Up) e per la bisettrice dell'angolo retto definito dagli assi x e -z (z negativo).
Traslazione di una Formula
Definisco traslata di una data formula, la stessa formula in cui però la stessa sequenza di mosse viene applicata a facce diverse del cubo ottenendo così una differente espressione per la stessa formula.in genere si utilizza una traslazione per eseguire la formula su certe facce anziché su altre, a seconda delle preferenze personali; traslando una sequenza di mosse infatti in genere si arriva ad una differente modalità di attuazione dei gesti necessari per eseguire la formula stessa.
Coniugazione
Ogni formula coinvolge alcuni pezzi in determinate precise posizioni ma potrebbe accadere che i cubetti che occorrerebbe posizionare od orientare si trovino in posizioni differenti da quelle su cui agisce la formula stessa.Con alcune metodologie utilizzate per risolvere il cubo potrebbe allora essere necessario posizionare i pezzi che si vogliono sistemare nelle posizioni specifiche in cui agisce la formula stessa; per far ciò si esegue una breve sequenza di mosse preparatorie (normalmente da una a massimo quattro mosse); tale sequenza preparatoria viene chiamata coniugazione.
Questo avviene per esempio se si vogliono ribaltare 2 spigoli adiacenti posizionandoli in asse con la faccetta centrale (in opposizone) mediante una semplice coniugazione di due mosse per poi applicare la Rube Move.
Dopo aver applicato la formula occorrerà naturalmente effettuare l'anticoniugazione, ovvero eseguire la sequenza preparatoria in modo inverso, cioè partendo dall'ultima mossa ed arrivando alla prima ed eseguendo tutte le mosse con una rotazione contraria a quella usata nella coniugazione, onde ripristinare il corretto ordinamento dei pezzi alterato dalla coniugazione.
Quindi la successione di azioni da eseguire sarà:
Coniugazione Formula Anticoniugazione
Questa è una delle tecniche fondamentali con cui si può individuare una formula (vedi genesi delle formule risolutive).
Concatenazione di Formule - espressioni
La concatenazione di formule è un concetto analogo a quello della concatenazione di stringhe.Con concatenazione di due formule si intende semplicemente l'esecuzione in successione delle due formule; formalmente utilizzerò il segno +, ossia
concatenazione di formula_1 e formula_2 = formula_1 + formula_2
Andando a scrivere una espressione delle formule si scriveranno semplicemente le mosse della prima formula seguite dalle mosse della seconda formula, ossia
espressione_1 espressione_2
L'espressione di una formula è una delle possibili applicazioni pratiche della formula ovvero è una possibile rappresentazione della formula; cioé per una data configurazione da risolvere e fissato l'orientamento del cubo un'espressione della formula è l'attuazione della formula utilizzando certe particolari facce del cubo.
Ad una data formula corrispondono molte possibili espressioni che verranno applicate definendo diversi orientamenti (diverse impugnature) del cubo; da una qualunque espressione si possono ottenere tutte le altre espressioni di quella data formula mediante traslazione e/o applicazioni inverse o simmetriche della prima.
Chiarendo con un esempio per orientare tre angoli senza cambiarne la posizione e senza muovere gli spigoli si può utilizzare la concatenazione di una Sune e di una Allan, cioé
Formula = Sune + U2 + y + Allan
ed una delle possibili espressioni di questa formula mantenendo l'angolo con orientamento corretto in ULF sarà:
espressione = (espressione_1) U2 y (espressione_2) = (R U R' U R U2 R') (U2) y (F2 U' V U2 V' U' F2)
Un'altra espressione della stessa formula mantenendo l'angolo orientato correttamente sempre in ULF, valida ma priva di reale utilità ed utilizzata solo per chiarire il concetto, potrebbe allora essere:
espressione2 = y2 (espressione2_1) U2 y (espressione_2) = y2 (L U L' U L U2 L') (U2) y' (F2 U' V U2 V' U' F2)
Nel seguito per non complicare inutilmente il discorso considererò un'espressione della formula e la formula stessa come se fossero la stessa cosa e non distinguerò tra formula e una sua particolare rappresentazione (espressione).
Nota sulla forma compatta:
Riporto una forma compatta delle formule, quando possibile, utilizzata esclusivamente per facilitarne la memorizzazione e la lettura; consente inoltre di vedere facilmente certe proprietà della formula stessa.Nella forma compatta utilizzo la notazione:
(Formula)*n che sta' per Formula Formula .... Formula (n volte)
ovvero si intende la formula eseguita N volte
ovvero n concatenazioni della stessa formula.
Nota ancora che la forma mnemonica può riportare a volte una mossa in più, inserita solo per poterla esprimere in modo formale e che viene comunque annullata da una immediata contro mossa.
Da notare infine che la forma mnemonica risulta spesso più lenta da essere eseguita che non la forma estesa (a causa di mosse aggiunte e di mosse come U2 divisa in U + U); quando ciò non avvenga utilizzo normalmente la sola forma compatta, altrimenti le riporto entrambe.
Riassunto delle convenzioni usate per la notazione
Riporto qui un breve riassunto delle notazioni utilizzateLe 6 faccette centrali non possono cambiare la loro mutua posizione e rappresentano il nostro sistema di riferimento - ovvero in ogni istante definiscono il colore della faccia su cui si trovano
- Upper or top face = U
- Down or bottom face = D (opposta ad Up)
- Left face = L
- Right face = R
- Front face = F
- Back face = B (opposta a Front)
- Una rotazione di 90 gradi oraria di una faccia, diciamo della faccia U, si indica con U
- Una rotazione di 90 gradi antioraria di una faccia si indica con U'
- Una rotazione di 180 gradi si indica con U2
- La rotazione dello strato centrale verticale (tra L e R) si indica con M (Middle slice) e se ne stabilisce il verso orario guardandolo da sinistra (dal lato Left)
- La rotazione dello strato centrale orizzontale (tra U e D) si indica con E (Equator Slice) e se ne stabilisce il verso orario guardandolo dalla faccia Down
- La rotazione dello strato centrale verticale parallelo alla Front (tra F e B) si indica con S, e se ne definisce il verso orario guardandolo dalla faccia Front
x significa posizionare il cubo eseguendo una rotazione oraria di 90 gradi intorno all'asse x (asse perpendicolare alle facce Left e Right positivo se visto da Right)
x' significa posizionare il cubo eseguendo una rotazione antioraria di 90 gradi intorno all'asse x (asse perpendicolare alle facce Left e Right e positivo quando visto da Right)
y significa posizionare il cubo eseguendo una rotazione oraria di 90 gradi intorno all'asse y (asse perpendicolare alle facce Up e Down, positivo quando visto da Up)
y' significa posizionare il cubo eseguendo una rotazione oantioraria di 90 gradi intorno all'asse y (asse perpendicolare alle facce Up e Down, positivo quando visto da Up)
Rw' (Right with) è la rotazione antioraria contemporaneamente dello strato Right e dello strato centrale M (resta fermo solo lo strato Left).
Con riferimento alla colonna Posizioni Coinvolte delle tabelle
- con due lettere mi riferisco ad uno spigolo dandone le coordinate
- con tre lettere indico un angolo riferendomi alle sue coordinate
Interpretazione delle figure
Nelle figure esplicative delle formule viene rappresentata l'ultima faccia ancora da risolvere (faccia Up); naturalmente mi riferisco al terzo ed ultimo strato di un generico metodo a strati.I brevi segmenti laterali gialli evidenziano l'orientamento della faccetta del pezzo prima di applicare la formula; quella faccetta si verrà a trovare orientata verso la faccia Up (nella eventuale nuova posizione) dopo applicata la formula; le frecce rappresentano lo spostamento che subirà il pezzo per effetto della stessa formula.
Interpretazione delle parentesi nelle formule
Formule sugli spigoli
Posizioni coinvolte |
Formula |
Descrizione |
 UF, UB |
(M' U)*3 U (M U)*3 U (Rube Move) oppure y (M' U)*3 M2 (U M')*3 U2 oppure y (M' U)*4 (M' U')*4 |
ribalta (orienta) i due spigoli |
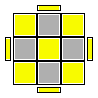 UF, UB, UR, UL |
(M' U)*3 M' U' (M' U)*3 M' U' oppure R2 D F2 (M' U)*4 F2 D' R2 oppure (M' U)*4 (M U)*4 |
ribalta (orienta) i quattro spigoli |
 UL, UR, UF |
M U M' U2 M U M' Forma alternativa: R L' B R' L U2 R L' B R' L |
Permuta i tre spigoli in senso orario, ribaltandone due |
 UL, UR, UF |
M U' M' U2 M U' M' Forma alternativa: R L' B' R' L U2 R L' B' R' L |
Permuta i tre spigoli in senso antiorario, ribaltandone due (simmetrica della precedente) |
 UL, UR, UF |
F2 U M' U2 M U F2 Forma alternativa: F2 U R' L F2 R L' U F2 |
Allan Permuta i tre spigoli in senso orario, senza cambiarne l'orientamento |
 UL, UR, UF |
F2 U' M' U2 M U' F2 Forma alternativa: F2 U' R' L F2 R L' U' F2 |
Allan simmetrica Permuta i tre spigoli in senso antiorario, senza cambiarne l'orientamento |
 (UF, UB), (UL, UR) |
M2 U M2 U2 M2 U M2 Forma compatta: (M2 U)*2 (U M2)*2 altre formule: R2 D2 B2 D (L2 F2)*3 D' B2 D2 R2 R L U2 R' L' F' B' U2 F B [cube.misto.cz] |
Scambia le due coppie di spigoli (UF, UR) e (UB, UL) senza cambiarne l'orientamento |
Nota sulle forme alternative:
Le forme alternative nelle tabelle sono LE STESSE FORMULE, espresse utilizzando una diversa notazione.Osserva che l'esecuzione delle due mosse R L' equivale a ruotare la fetta centrale del cubo in senso contrario (V').
C'è da osservare che utilizzando la notazione R L' il sistema di riferimento rimane invariato (in quanto la faccetta centrale della faccia up non si sposta) mentre utilizzando la forma equivalente M il sistema di riferimento si sposta, in quanto quella che prima era la faccia back dopo aver applicato M diventa la faccia U (cioè la faccetta centrale della faccia Back è passata in posizione Up) e a questo nuovo riferimento si riferiscono le successive mosse applicate nella formula; l'effetto delle mosse è identico, sia utilizzando la dizione R L' che la dizione M ma cambia l'espressione della formula.
Siccome cambia il sistema di riferimento potrebbe cambiare qualcosa anche nella attuazione dei movimenti necessari per eseguire la formula stessa.
Chiarendo con un esempio pratico il cambio del sistema di riferimento:
F2 U R' L F2 R L' U F2
è equivalente a
F2 U M' U2 M U F2
e NON a
F2 U M F2 M' U F2
Ho inserito l'espressione con R L' o R' L per facilitare la comprensione della formula.
Talvolta si sfrutta la definizione della mossa Rw (vedi pagina notazione) per formalizzare la mossa dello strato centrale M in una forma diversa che rispecchi anche uno dei modi effetivamente utilizzati per eseguire la mossa:
M' = Rw R' = R' Rw
M = Rw' R = R Rw'
Tale forma potrebbe apparire più complicata da leggere ma vuole evidentemente suggerire una delle possibili modalità pratiche di attuazione della mossa.
Formule sugli angoli
Posizioni coinvolte |
Formula |
Descrizione |
 URB, ULF, ULB |
(U) R U' L' U R' U' L |
Niklas Permuta i tre angoli in senso antiorario ruotandoli con spin +1/3 si tratta in effetti di U + Niklas |
 ULB, URF, URB |
(U') L' U R U' L U R' |
Niklas simmetrica Permuta i tre angoli in senso orario ruotandoli con spin -1/3 si tratta in effetti di U' + Niklas simmetrica |
 ULF, ULB |
(U R U' R' U R U') L' (U R' U' R U R' U') L forma compatta (che riporta 2 mosse in più): (U R U' R')*2 L' (R U R' U')*2 L |
Double Niklas Ruota su sé stessi (orienta) i due angoli, ULB con spin +1/3 e ULF con spin -1/3 |
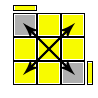 URF, ULB, ULF, URB |
forma compatta: L' D2 (U R U' R')*3 D2 L |
scambia le 2 coppie di angoli in diagonale (URF, ULB) e (ULF, URB) |
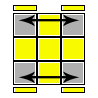 URF, ULF, URB, ULB |
forma compatta: F (U R U' R')*3 F' |
scambia le 2 coppie di angoli adiacenti (URF,ULF) e (URB,ULB) |
Nota 1:
Nelle due formule per lo scambio di due coppie di angoli, l'inizio delle due formule, rispettivamente L' D2 ed F sono a tutti gli effetti due coniugazioni, dove le anti coniugazioni sono le chiuse delle due formule D2 L e F'.
Anche nello formula dello scambio di due coppie di spigoli R2 D2 B2 D rappresenta la coniugazione e D' B2 D2 R2 l'anticoniugazione.
Nota 2
Riguardo la formula nella tabella (U R U') L' (U R' U') L questa può concettualmente essere pensata come
(U R U' R') L' (R U R' U') L da cui poi deriva anche quella per ruotare sul posto due angoli con spin opposti
(U R U' R')*2 L' (R U R' U')*2 L
Formule Miste su spigoli ed angoli
Posizioni coinvolte |
Formula |
Descrizione |
UF, UL, ULF, DRB, URB, RB |
R' U' R U B U' B' Forma Inversa: B U B' U' R' U R |
Scambia la coppia di spigoli UF,UL e la coppia di angoli ULF,DRB ruota inoltre URB e ribalta RB |
UF, UL, ULF, DRB, URB |
(R' U' R U B U' B')*2 Forma Inversa: (B U B' U' R' U R)*2 |
Ribalta la coppia di spigoli UF,UL ruota su se' stessi di +1/3 (-1/3 la inversa) gli angoli ULF,DRB, URB |
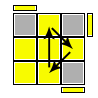 UF, UR, UB, URF, URB, ULB |
R U R' U R U2 R' (U2) |
Sune Permuta i tre spigoli in senso orario senza ribaltarli e orienta i tre angoli dandogli spin +1/3 si tratta in effetti di Sune + U2 |
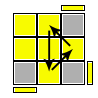 UF, UR, UB, URF, URB, ULF |
R' U' R U' R' U2 R (U2) |
Sune simmetrica Permuta i tre spigoli in senso antiorario senza ribaltarli e orienta i tre angoli dandogli spin -1/3 si tratta in effetti di Sune simmetrica + U2 |
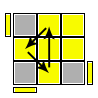 UF, UL, UB, URF,ULF, ULB |
R U2 R' U' R U' R' (U2) |
Anti Sune (Sune Inversa) Permuta i tre spigoli in senso antiorario senza ribaltarli e orienta i tre angoli dandogli spin -1/3 si tratta in effetti di Anti Sune + U2 |
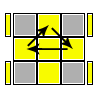 UR, UL, UB, URF,ULF, URB, ULB |
R U R' U R (U' R' U R) U2 R' |
Double Sune Orienta i 4 angoli e permuta tre spigoli |
Nelle tre tavole precedenti sono raggruppate alcune formule che giudico molto semplici da apprendere e sicuramente le prime che consiglierei di imparare.
La tavola più in basso raggruppa in modo eterogeneo alcune altre interessanti formule non troppo difficili da eseguire
altre formule
 UF, UR, UB |
R (U R') U' Rw (R' U) (R U') Rw' = R U R' U' M' U R U' Rw' = (R U R' U') M' (U R U' R') M oppure x M U R' U' M' U R U' x' |
Permuta i tre spigoli in senso antiorario ribaltandone due |
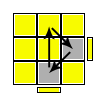 UF, UR, UB |
Rw (U R') U' Rw' R U (R U') R' = M' (R U R' U') M (U R U' R') |
Permuta i tre spigoli in senso orario ribaltandone due |
 URB, ULF, ULB |
x (U R') (U' L) U (R U') Rw' = x U R' U' L U R U' Rw' = x U R' U' L U R U' L' x' |
Evelyn Permuta i tre angoli in senso orario ribaltandone due |
 URB, ULF, ULB |
Rw (U R') U' L' U (R U') x' = x L U R' U' L' U R U' x' |
Evelyn inversa Permuta i tre angoli in senso antiorario ribaltandone due |
 ULF, URF, URB |
(Lw U' R) D2 (R' U) R D2 R2 x |
Permutazione antioraria di tre angoli senza cambiarne l'orientamento |
 ULB, URF, URB |
(Lw' U R') D2 (R U') R' D2 R2 x |
Permutazione oraria di tre angoli senza cambiarne l'orientamento |
 (UF, UB), (UR, UL) |
Rw' R U R (U R') U' Rw2 (R'2 U) (R U') Rw' (U') |
scambia le due coppie di spigoli opposti ribaltandoli |
 (UF, UL), (UR, UB) |
M2 U M' U2 M2 U2 M' U' M2 Forma compatta: M2 U (M' U2 M')*2 U' M2 |
scambia le due coppie di spigoli adiacenti senza cambiarne l'orientamento |
PLL - Permute Lat Layer - Posizionamento - Possibili Configurazioni
Nella fase iniziale del terzo ed ultimo strato potrete incontrare un numero piuttosto limitato di differenti tipologie di configurazioni.N.B.
Qui osservo esclusivamente il posizionamento dei pezzi, prescindendo da ogni loro possibile orientamento.
Mi riferirò al caso in cui si osservano gli spigoli (e quindi al caso in cui cominciate a risolvere il problema del posizionamento dei pezzi nell'ultimo strato partendo dagli spigoli) ma lo stesso identico discorso vale se si osservano gli angoli invece degli spigoli.
Occorre eseguire una mossa preparatoria (passo preliminare) affinché la casistica proposta sotto risulti coerente [infatti se tutti gli spigoli sono fuori posizione ruotando l'Ultimo Strato questo porterà ad uno tra due differenti casi: tutti e 4 gli spigoli in posizione corretta oppure uno scambio tra due spigoli opposti]
Passo Preliminare:
- ruota la Up in modo da mettere in posizione corretta almeno uno spigolo.
Possibili tipologie di configurazioni per gli spigoli
- 4 spigoli posizionati correttamente
- 1 solo spigolo posizionato correttamente - gli altri tre spigoli devono permutare in senso orario od antiorario
- 2 soli spigoli in posizione opposta rispetto al centro posizionati correttamente - scambio di due spigoli opposti (scambio misto)
- 2 soli spigoli in posizione adiacente posizionati correttamente - scambio di due spigoli adiacenti (scambio misto)
In corrispondenza dei casi 1. e 2. avremo le seguenti possibili tipologie di configurazioni per gli Angoli:
- 4 angoli in posizione corretta
- Permutazione tra tre angoli
- Doppio scambio delle due coppie di angoli adiacenti
- Doppio scambio delle due coppie di angoli sulla diagonale
In corrispondenza dei casi 3. e 4. avremo le seguenti possibili tipologie di configurazioni di Angoli:
- Scambio di una coppia di angoli adiacenti
- Scambio di una coppia di angoli sulla diagonale
- Configurazione "ruotata" con i 4 angoli tutti in posizione sbagliata
- Configurazione "a clessidra" con i 4 angoli tutti in posizione sbagliata
La cosa da osservare è che trovandosi in una situazione con scambio misto (casi 3 e 4 per gli spigoli) con una semplice rotazione della faccia Up vi potete portare in una delle due situazioni:
- un solo spigolo è in posizione corretta con una mutua rotazione degli altri tre spigoli (se i due spigoli scambiati sono in posizione adiacente rispetto al centro)
- nessuno spigolo è in posizione corretta con due coppie di spigoli scambiati (se i due spigoli scambiati sono in posizione opposta rispetto al centro)
mentre gli angoli avranno a questo punto una delle configurazioni che derivano dai casi 1. e 2. degli spigoli
Nella nuova situazione cioè non incontrerete più una situazione "mista" intesa nel senso di uno scambio di due coppie di tipo differente; quindi non vi occorrerebbero neanche le formule miste per lo scambio delle due coppie una di angoli ed una di spigoli.
Ovviamente dipende dal metodo scelto se si usano anche le formule miste o meno ed il tutto viene deciso eseguendo una semplice mossa sulla faccia Up prima di comiciare la fase di posizionamento dei pezzi nell'ultimo strato.
Di fatto normalmente tutti i metodi a strati semplici che ho visto evitano di risolvere direttamente il caso misto.
La Rurubub
Un discorso a parte merita la bellissima formulaR' U' R U B U' B'
di ciclicità 12 e la sua inversa
B U B' U' R' U R
che coinvolge gli stessi pezzi ruotandoli però tutti in verso contrario
La rurubub è una formula mista (nel senso che scambia una coppia di spigoli ed una coppia di angoli) se applicata un numero dispari di volte ed è una formula sugli spigoli o sugli angoli se applicata 4 o 6 o 8 volte.
Questa formula applicata una volta come detto (vedi tabella delle formule) scambia una coppia di spigoli ribaltandone uno e scambia una coppia di angoli ed è questo l'utilizzo più semplice che se ne può fare, normalmente da applicare nella prima fase di ordinamento dell'ultima faccia (utilizzando sempre una opportuna coniugazione, la più semplice è o R o B', in modo da non coinvolgere i pezzi dei due strati sottastanti già ordinati);
applicando la stessa formula 2 volte le due coppie tornano al loro posto; i due spigoli risultano ribaltati e i tre angoli ruotati di +1/3;
applicata 4 volte l'effetto e` di ruotare su sé stessi di -1/3 i tre angoli!
applicata 6 volte l'effetto e` di ribaltare i 2 spigoli!!
applicata 8 volte ruota su sé stessi i tre angoli di +1/3
applicata 10 volte ribalta i due spigoli e ruota i tre angoli di -1/3
applicata 12 volte il cubo torna infine nella configurazione iniziale;
invece di applicare 8 o piu` volte la formula diretta conviene evidentemente utilizzare 4, 2 o 1 volta la formula inversa: B U B' U' R' U R.
Per la rotazione sul posto di tre angoli la rurubub o la sua inversa applicata 4 volte (28 mosse) è di poco più efficiente della formula di rotazione di due angoli applicata 2 volte (32 mosse), ma una soluzione più efficiente risulta essere per esempio la concatenazione di una Sune e di una Allan (Sune + Allan) che permette di orientare tre angoli con 15 mosse.
In ogni caso la rurubub è piuttosto complessa coinvolgendo numerosi pezzi e va' spesso utilizzata utilizzando una coniugazione per portare qualche pezzo dalla faccia Up (che è l'ultima faccia quando si esegue la formula) sull'angolo DRB e sullo spigolo RB prima di applicarla onde non muovere i pezzi già ordinati dei primi due strati.
Questa formula è potente in quanto è molto corta e semplice da eseguire.
Può essere utile nella prima fase di completamento dell'ultima faccia per scambiare una coppia di spigoli e di angoli o applicata due volte per ribaltare una coppia di spigoli; in una fase più avanzata di apprendimento si può utilizzare anche per controllare la rotazione sul posto di 1/3 di tre angoli (scegliendo se usare la rurubub o la buburur) mentre si ribaltano i due spigoli; in una fase ancora più avanzata mentre si decide di usare la rurubub o la buburur per raddrizzare i due spigoli o mantenerli ribaltati mentre si scambiano di posto si potrebbe controllare anche lo scambio della coppia di angoli tramite una opportuna coniugazione che però a questo punto diventa assai complessa da gestire.
Ovviamente se non si utilizzano le coniugazioni (tranne quelle minimali per evitare di scomporre i due strati inferiori che devono sempre essere eseguite quando si usa questa formula) si dovranno eseguire più formule per conseguire lo stesso risultato.
Quindi la rurubub va' sempre pensata almeno con una delle due coniugazioni più semplici:
R ( R' U' R U B U' B') R'
oppure
B' ( R' U' R U B U' B') B
indico sempre tutte le mosse per maggiore chiarezza espositiva anche se non andrebbero eseguite.
Se siete arrivati a leggere fin qui ed avete ancora la forza di domandarvi perché tenere la formula in questa forma facendola agire su quei due pezzi lì dietro BR e DRB, direi che questo permette di scegliere se nella coniugazione mandare giù la faccia Back o la faccia Right, in modo da avere maggiore scelta per i pezzi da usare (in particolare per l'angolo da scambiare o girare); inoltre in questa forma la formula inversa appare in modo perfettamente speculare, cioè la simmetrica è uguale alla inversa! Questo da' alla formula stessa una particolare bellezza estetica e facilita l'utilizzo dell'inversa, che anzi risulta più veloce da essere eseguita della forma diretta.
Se sapete risolvere il cubo con un qualche metodo a strati probabilmente già conoscete ed usate la Rurubub:
si riconoscono infatti la F R U R' U' F' e la F U R U' R' F', usatissime per realizzare l'orientamento degli spigoli come primo passo della risoluzione del terzo strato.
Dalla F R U R' U' F' si ottiene con una semplice traslazione R B U B' U' R' che è evidentemente uguale a R (B U B' U' R' U R) R' in cui vengono eliminate le ultime tre mosse, R ed R' perché evidentemente si annullano tra loro e quindi non si eseguono mai e la U in quanto nella fase di orientamento in cui viene applicata la formula nei metodi semplificati non interessa riposizionare correttamente i pezzi sulla faccia Up ma solo orientarli.
Dalla F U R U' R' F' con la medesima traslazione si ottiene R U B U' B' R' che è equivalente a R (R' U' R U B U' B') R' in cui si omettono le prime tre mosse, (R ed R' si eliminano tra loro e U' si può omettere in quanto la sua eliminazione porta semplicemente a far agire la formula su dei pezzi differenti); se preferite potete ricondurla alla inversa della R (B U B' U' R' U R) R' eliminando le ultime tre mosse.
Sono quindi entrambe una rurubub cui viene applicata una qualche particolare coniugazione e traslazione.
Inoltre con una assegnata coniugazione la rurubub è correntemente utilizzata in almeno sette delle formule di orientamento nel metodo Fridrich ed in effetti le due precedenti formule utilizzate per l'orientamento degli spigoli nei metodi semplificati sono proprio due di queste formule dell'OLL del Fridrich completo; sono due formule che cambiano anche l'orientamento di alcuni angoli, e nel Fridrich completo vanno applicate a due particolari configurazioni in cui si devono orientare contemporaneamente angoli e spigoli mentre le formule utilizzate per orientare solo gli spigoli sono altre (due utilizzabili per questo scopo sono riportate nella tabella altre formule); nel sistema semplificato invece non ci importa se gli angoli cambiano orientamento, in quanto li orienteremo correttamente solo nel passo successivo; nei metodi semplificati si utilizzano queste in luogo delle vere formule per l'orientamento dei soli spigoli in quanto più brevi e semplici da eseguirsi.
In effetti si possono trovare almeno 13 formule di orientamento semplicemente utilizzando la rurubub con qualche coniugazione.
Formule di Orientamento deducibili dalla rurubub
Queste sono formule di solo orientamento utilizzabili nel metodo di risoluzione Fridrich (cioé utilizzabili per orientare i pezzi prima di effettuare il loro posizionamento); viene preso in esame il solo orientamento e non vengono quindi indicate le permutazioni dei pezzi che pure sono presenti.
Per alcune di queste configurazioni esistono formule più brevi che eseguono lo stesso lavoro di orientamento, ma sette di queste sono effettivamente adottate nel metodo Fridrich in quanto evidentemente le più efficienti che si possano trovare per quel particolare stato (le prime sette della lista).
A volte preferisco utilizzare la forma con la rurubub ed a volte quella con la fufurur a seconda di quale trovo più comodo eseguire.

F U R U' R' F' = R (R' U' R U B U' B') R'
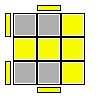
F R U R' U' F' = y' R (B U B' U' R' U R) R'

B' U' R' U R B = y' B' (B U B' U' R' U R) B
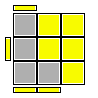
R' U' F U R U' R' F' R = y' B' R (R' U' R U B U' B') R' B
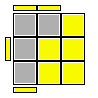
R U B' U' R' U R B R' = R B' (B U B' U' R' U R) B R'
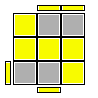
R' F R U R' U' F' U R = y' B' R (B U B' U' R' U R) R' B

R B' R' U' R U B U' R' = R B' (R' U' R U B U' B') B R'

Rw' R2 B U B' U' R' U M' = M R (B U B' U' R' U R) R' M'
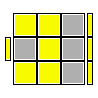
M U' R U B U' B' Rw R2 = M R (R' U' R U B U' B') R' M'
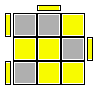
S' B' R' U' R U B U' S = S' B' (R' U' R U B U' B') B S

S' U B' U' R' U R B S = S' B' (B U B' U' R' U R) B S

M B' U' R U B U' B' R' B M' = M B' R (R' U' R U B U' B') R' B M'
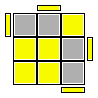
M B' R B U B' U' R' U B M' = M B' R (B U B' U' R' U R) R' B M'
F (U R U' R') * 2 F' = R (R' U' R (U B U' B') * 2) R' (U)
F (R U R' U') * 2 F' = (U') R ((B U B' U') *2 R' U R) R'
F (R U R' U') * 3 F' = (U') R ((B U B' U') *3 R' U R) R'
La R B U B' U' R' è uguale a R (B U B' U' R' U R) R' (a meno di R ed R' e dell'ultima mossa sulla Up che in fase di orientamento non è necessario usare).
Dalla R' U' F' U F R si ottiene la traslata B' U' R' U R B la cui inversa è B' R' U' R U B che evidentemente è uguale a B' (R' U' R U B U' B') B (a meno di R ed R' e dell'ultima mossa sulla Up che in fase di orientamento non è necessario usare)
Dalla L U F U' F' L' si ottiene la traslata R U B U' B' R' la cui inversa è la R B U B' U' R' che è evidentemente uguale alla R (B U B' U' R' U R) R' (a meno di R ed R' e dell'ultima mossa sulla Up che in fase di orientamento non è necessario usare) .
La traslata della F R U R' U' F' è L F U F' U' L' la quale è l'inversa della L U F U' F' L'.
La F U R U' R' F' è semplicemente l'inversa della F R U R' U' F'.
Così avete visto che la rurubub è "una vecchia conoscenza" :)
Grazie alla sua versatilità e brevità è secondo me la vera regina delle formule risolutive del cubo di Rubik pur se tutt'altro che appariscente, anzi la mia prima impressione vedendo questa formula (una delle prime 3 o 4 che ho imparato un secolo fa') è che creasse una gran confusione.
La rurubub consentirebbe di risolvere agevolmente il terzo strato utilizzando solo tre formule, congiuntamente per esempio con le due formule (importantissime) per la permutazione di tre angoli (la Niklas o la equivalente che io uso) e per la rotazione sul posto di due angoli (derivata dalla formula precedente), ma consiglierei di fare uno sforzo addizionale per imparare anche qualche altra formula.
A definitiva prova della potenza di questa formula definisco il seguente enunciato:
Teorema (della Rurubub):
Utilizzando unicamente la Rurubub e delle semplici coniugazioni è possibile risolvere completamente l'ultimo strato (qualunque sia la sua configurazione) posizionandone ed orientandone correttamente tutti gli spigoli e gli angoli!
Questo grazie alla peculiarità della formula che scambia entrambi i tipi di pezzi e li orienta in modo asimmetrico (non gira i pezzi tutti insieme il che consente applicando più volte la formula, cambiando la posizione del cubo ed utilizzando ad ogni applicazione della formula differenti coniugazioni, di ottenere qualunque combinazione di rotazioni e di scambi).
dimostrazione del Teorema:
Una volta accettate per vere le leggi fisiche del cubo, per ottenere una semplice dimostrazione di quanto ho asserito è sufficiente dimostrare che è possibile realizzare con questa sola formula e delle semplici coniugazioni tutte le mosse atomiche.
Per dimostrare quest'ultimo fatto è sufficiente trovare per ogni mossa atomica definita dalle leggi fisiche del cubo una particolare sequenza di rurubub e coniugazioni che la realizzi.
Considerato che si può pensare di attuare prima il posizionamento di tutti i pezzi (senza badare all'orientamento) e successivamente il loro corretto orientamento (facendo attenzione a non alterare le posizioni raggiunte dai pezzi), nella dimostrazione, per semplicità, in tutte le formule sul posizionamento (scambio o permutazione) mi disinteresso dell'orientamento senza perdita di generalità, mantenedo cioè comunque la dimostrazione valida.
Innanzitutto decido di utilizzare anche l'inversa e definisco quindi la relazione tra le due espressioni; essendo il ciclo della Rurubub 12 si ha:
BUB'U'R'UR = (R'U'RUBU'B')*11
questi sono dei semplici esempi di come realizzare le mosse atomiche
Posizionamento
- lo scambio di due coppie di pezzi
scambio di una coppia di angoli e di una coppia di spigoli (misto):
R (R'U'RUBU'B') R';
scambio di 2 coppie di angoli:
R (R'U'RUBU'B') R' y M R (BUB'U'R'UR) R' M';
scambio di 2 coppie di spigoli:
R (R'U'RUBU'B') R' y2 R (R'U'RUBU'B') R': - la permutazione di tre pezzi
3 angoli:
R (R'U'RUBU'B') R' B' R (BUB'U'R'UR) R' B ;
3 spigoli:
R (R'U'RUBU'B') R' S' B' (R'U'RUBU'B') B S
- il ribaltamento di due spigoli (orientamento di due spigoli) senza alterare la posizione dei pezzi
R (R'U'RUBU'B')*6 R' - la rotazione su sé stessi con uguale spin di tre angoli (orientamento di tre angoli) senza alterare la posizione dei pezzi
R (R'U'RUBU'B')*4 R' - la rotazione su sé stessi con spin opposti di due angoli (orientamento di due angoli) senza alterare la posizione dei pezzi
R (R'U'RUBU'B')*2 R' B' R (BUB'U'R'UR)*2 R' B
All'atto pratico non occorrono molte iterazioni della formula per risolvere il terzo strato; normalmente, volendo dare un'idea quantitativa, possono occorrere tra 4 e 20 iterazioni, cioè 20 - 120 mosse; mi piacerebbe un giorno formalizzare un algoritmo che segua questa tecnica "inconsueta" che però non può essere competitiva con gli altri metodi anche se imparata alla perfezione in quanto occorre molta più osservazione della configurazione (e quindi tempo) per decidere come applicare la formula; si può anche dire che ad ogni particolare coniugazione applicata alla rurubub corrisponda una formula e in definitiva il metodo consiste di numerose formule; di fatto però tali formule sono determinabili abbastanza facilmente.
Corollario al Teorema :
.. avendo molta pazienza.. utilizzando la Rurubub e delle semplici coniugazioni è possibile risolvere l'intero cubo partendo da una qualunque configurazione iniziale.
Naturalmente esistono altre formule che consentano di ottenere lo stesso risultato; il pregio della rurubub è quello di essere di sole 7 mosse.
La Sune
La Sune (vedi anche genesi formule) è una bella formula che prende questo nome nel metodo di Lars Petrus.Essendo piuttosto breve e rapida da essere eseguita è utile pensare a qualsiasi sua possibile applicazione e può essere utile in numerose differenti metodologie risolutive; queste quelle che mi vengono in mente:
- senza la chiusura viene utilizzata per l'orientamento degli angoli senza alterare l'orientamento degli spigoli e quando non sia ancora avvenuto il posizionamento di angoli e spigoli
- chiudendola con U2 può essere utilizzata per orientare tre angoli senza alterarne la posizione quando sia già stata effettuato l'orientamento degli spigoli ma non il loro posizionamento
- chiudendola con U2 si può usare per permutare tre spigoli già orientati, qualora sia già avvenuto il posizionamento degli angoli ma non il loro orientamento
- senza la chiusura si può utilizzare per permutare gli spigoli già orientati qualora gli angoli non siano ancora stati posizionati ed orientati
- senza chiusura ma aggiungendo una U come ottava mossa si può realizzare uno scambio di due spigoli già orientati, quando ancora gli angoli non siano stati né orientati né posizionati
La mossa U2 che ho chiamato chiusura è semplicemente una ottava mossa da eseguire, U2, a completamento (chiusura appunto) della formula cioé per riposizionare gli angoli nella giusta posizione.
La Sune senza chiusura ha ciclicità 6 e con la chiusura ciclicità 3.
La Sune si esprime con l'espressione
R U R' U R U2 R'
essendo U2 U' = U questa si può scrivere:
R U2 U' R' U R U2 R' = R U2 (U' R' U R) U2 R'
da cui si evince che la formula è costituita da
- coniugazione R U2
- sequenza base U' R' U R
- relativa anticoniugazione U2 R'
a conferma di ciò:
La Double Sune si scrive
R U R' U R (U' R' U R) U2 R' = R U2 (U' R' U R)*2 U2 R'
La Triple Sune si scrive
R U R' U R (U' R' U R) (U' R' U R) U2 R' = R U2 (U' R' U R)*3 U2 R'
La Double Sune è già chiusa (cioé gli angoli restano nella loro posizione) ed ha ciclicità 3; La triple Sune è invece eventualmente da chiudere con U2 (qualora interessi anche il posizionamento e non solo l'orientamento) e nella forma aperta ha ciclicità 2 ed in quella chiusa ciclicità 6.
La sequenza di mosse (U' R' U R) o la sua simmetrica (U R U' R') (simmetrica rispetto al piano passante per gli assi xy) o una delle due inverse, rispettivamente (R' U' R U) e (R U R' U'), o una qualche traslazione di una di queste, appare essere veramente fondamentale per definire molte semplici formule sugli angoli.
La Niklas
La Niklas, (vedi anche genesi formule) come molte formule "brevi" (di non più di 8 - 9 mosse), è una formula fondamentale; prende questo nome nel metodo di Lars Petrus e viene utilizzata in numerosi metodi risolutivi a cominciare dal Fridrich (nell'orientamento).Fondamentalmente realizza una permutazione antioraria di tre angoli dandogli uno spin +1/3 senza modificare posizione ed orientamento degli spigoli; ma si può anche dire che realizza lo scambio di due angoli.
La Niklas viene definita come
R U' L' U R' U' L
a questa si aggiungerà un'ulteriore mossa a seconda dell'uso che se ne vuole fare:
- R U' L' U R' U' L
Con la sola sequenza base realizza l'orientamento di tre angoli senza cambiare l'orientamento degli spigoli ma quando non sia ancora avvenuto il posizionamento di angoli e spigoli
- R U' L' U R' U' L (U)
Chiudendola con U si ottiene la permutazione di tre angoli ancora da orientare quando gli spigoli sono già posizionati ed orientati.
- R U' L' U R' U' L (U2)
Chiudendola con U2 esegue lo scambio di una coppia di angoli non ancora orientati quando gli spigoli non siano ancora stati posizionati ma solo orientati
In effetti il secondo ed il terzo punto (a meno del posizionamento degli spigoli) sono due modi di vedere la stessa cosa.
Infatti dando un'occhiata alle possibili configurazioni relativamente al posizionamento e scambiando gli angoli con gli spigoli (cioè esaminando prima il posizionamento degli angoli) le possibili configurazioni sono:
- 4 angoli posizionati correttamente
- 1 solo angolo posizionato correttamente - gli altri tre angoli devono permutare in senso orario od antiorario
- 2 soli angoli in posizione opposta posizionati correttamente - scambio di due angoli opposti (scambio misto)
- 2 soli angoli in posizione adiacente posizionati correttamente - scambio di due angoli adiacenti (scambio misto)
così nella pagina dove Lars definisce la Niklas lui si pone sempre nella situazione 4 ed applica la Niklas + U2 per scambiare i due angoli in ULF e ULB.
In pratica suggerisce di cercare se due angoli adiacenti hanno una faccetta dello stesso colore (non considerando la faccetta col colore dell'Ultima Faccia); in caso affermativo si posizionano questi due angoli sulla faccia del colore delle due faccette comuni; potrà accadere che i due angoli sono posizionati correttamente (e gli altri due angoli saranno in posizione corretta o scambiati tra loro) o sono scambiati (e gli altri due angoli saranno in posizione corretta).
Seguendo tale strategia di posizionamento il caso 2 non si presenta mai e si ricade o nel caso 1 o nel caso 4; se non si trova una coppia di angoli adiacenti che hanno in comune il colore di una faccetta (esclusa la faccetta del colore dell'Ultima Faccia) allora si ricade nel caso 3; Lars ritiene che questa strategia di individuazione delle posizioni degli angoli sia più veloce.
Sicuramente se incontrando il passo 4 si ruota la Up e si rieffettua la ricerca della permutazione da eseguire (come suggerisco nel metodo per principianti, la quale è sicuramente una strategia più "didattica" e comprensibile), i tempi si allungano; se si impara però a risolvere direttamente il caso 2 od il caso 4 a seconda di quello che si incontra per primo all'inizio della fase di posizionamento dei pezzi dopo aver eseguito un "veloce passo preliminare" (come spiego per esempio in "Jasmine Lee intermediate") potrebbe non essere così determinante seguire la strategia di Lars; tale strategia appare invece estremamente interessante se si esegue dapprima l'orientamento dei pezzi e successivamente il loro posizionamento, in quanto in tal caso appare immediato trovare (nel caso ci sia) una coppia di angoli che presentino una faccetta dello stesso colore su una delle 4 facce laterali e posizionare quindi tale coppia; seguendo tale tecnica inoltre non è necessario utilizzare anche la formula simmetrica, ma si esegue sempre solo la forma diretta.
La Niklas è definita dalla sequenza
R U' L' U R' U' L
la quale con l'aggiunta di U (come apertura o chiusura) permuta tre angoli e con l'aggiunta di U2 (come apertura o chiusura) scambia due angoli.
di fatto si può quindi utilizzare una delle due espressioni:
R U' L' U R' U' L (U) oppure (U) R U' L' U R' U' L
e
R U' L' U R' U' L (U2) oppure (U2) R U' L' U R' U' L
Per comprendere il perché di questa particolare simmetria occorre meglio evidenziare la struttura della formula ottenuta utilizzando la tecnica del commutatore:
la mia versione:
1) (3-cycle counterclockwise): (U) R U' L' U R' U' L = U R U' R' + L' + R U R' U' + L
2) (3-cycleclockwise): (U') L' U R U' L U R' = U' L' U L + R + L' U' L U + R'
sul sito di Lars Petrus:
1) (3-cycle clockwise): L' U R U' L U R' (U') = L' + U R U' R' + L + R U R' U'
2) (3-cycle counterclockwise): R U' L' U R' U' L (U) = R + U' L' U L + R' + L' U' L U
quindi chiamando la URU'R' sequenza base della formula 1) e chiamando L' sostituzione della formula 1)
e anche chiamando la U'L'UL sequenza base della formula 2) e chiamando R sostituzione della formula 2)
si vede che la differenza tra le due formule deriva dallo scambiare l'ordine in cui vengono eseguite la sequenza base e la sostituzione; tale scambio porta alla stessa formula ma con permutazione in verso contrario.
A riguardo vedi anche tecnica del commutatore.
La relazione pratica che si apprezza tra le due formule é che l'espressione per la Niklas che utilizzo nella tabella:
(U) R U' L' U R' U' L
è la simmetrica inversa della Niklas utilizzata da Petrus:
R U' L' U R' U' L (U)
Si osservi anche che dalla Niklas R U' L' U R' U' L la simmetrica e la inversa coincidono nella L' U R U' L U R'.
Nota che in effetti chiamo Niklas la U + Niklas e questo potrebbe generare confusione, ma preferisco utilizzare la forma della Niklas chiusa con la U come formula di riferimento in quanto è questa la forma che porta al corretto riposizionamento degli angoli e quindi è una formula risolutiva secondo la definizione intuitiva che ho dato all'inizio di questa pagina; insomma preferisco dire semplicemente Niklas piuttosto che usare la dizione corretta U + Niklas; del resto anche l'altra forma che si trova spesso utilizzata in altre spiegazioni e che esegue lo scambio di due angoli viene spesso definita semplicemente come Niklas, mentre invece è la Niklas + U2 e quindi anche quella risulta una dizione inesatta.